Question

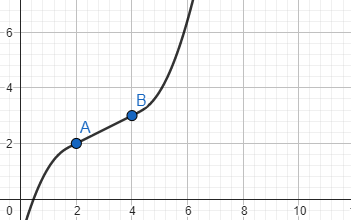
Auf Basis dieser Definitionen, wie viele Wendepunkte hat folgender Graph?Das Stück zwischen den beiden Punkten ist eine Gerade. Es ist keine Funktionsgleichung angegeben.
Ich weiß, dass dieser Graph keine Wendestellen besitzt, aber ich weiß nicht wie man das begründen kann.

Gegeben seien folgende Definitionen von "strenger Monotonie", von "Links-" bzw. "Rechtskurve" und von "Wendepunkt":

Defintion: Die Funktion f sei auf einem Intervall I definiert, Wenn für alle x1,x2 aus I gilt:
as x1<x2 folgt f(x1)<f(x2) dann heißt f streng monoton wachsend in I
as x1<x2 folgt f(x1)>f(x2) dann heißt f streng monoton fallend in I

Definition: Die Funktion sei au einem Intevall I definiert und differenzierbar. Wenn f´ auf I streng monoton wachsend ist, dann ist der Graph eine Linkskurve;
wenn f´ auf I streng monoton fallend ist, dann ist der Graph eine Rechtsskurve.

Definition: Dei Funktion f sei auf einem Intervall I definiert, differenzierbar und x0 sei eine innere Stelleim Intervall I.
Eine Stelle x0, bei der der Graph von f von einer Linkskurve in eine Rechtskurve übergeht oder umgekehrt, heißt Wendestelle von f.
Der zugehörige Punkt W(x0|f(x0) heißt Wendepunkt des zugehörigen Graphen.

Answer 1

Das Stück zwischen den beiden Punkten ist eine Gerade.

Dann ist \(f'(x)\) zwischen \(A\) und \(B\) konstant.

aus x1<x2 folgt f(x1)<f(x2) dann heißt f streng monoton wachsend in I
ais x1<x2 folgt f(x1)>f(x2) dann heißt f streng monoton fallend in I

Dann ist \(f'(x)\) zwischen \(A\) und \(B\) weder streng monoton wachsend, noch streng monoton fallend.

Wenn f´ auf I streng monoton wachsend ist, dann ist der Graph eine Linkskurve;
wenn f´ auf I streng monoton fallend ist, dann ist der Graph eine Rechtsskurve.

Dann ist der Graph von \(f\) zwischen \(A\) und \(B\) weder eine Linkskurve, noch eine Rechtskurve.

Eine Stelle x0, bei der der Graph von f von einer Linkskurve in eine Rechtskurve übergeht oder umgekehrt, heißt Wendestelle von f.

Dann hat \(f\) zwischen \(A\) und \(B\) keine Wendestellen.

Der zugehörige Punkt W(x0|f(x0) heißt Wendepunkt des zugehörigen Graphen.

Dann hat \(f\) zwischen \(A\) und \(B\) keine Wendepunkte.

Answer 2

Die einzig interessanten Punkte sind A und B.

Doch weder geht in A der Graph von einer Rechts- in eine Linkskurve über,

noch von einer Links- in eine Rechtskurve. Das Gleiche gilt für B.

Der Graph besitzt keine Wendepunkte.