Aufgabe:
Ich habe ein gegebenen Bereich (Polytop) C im einfachsten Fall ein Rechteck mit nicht gleichlangen Seiten. Auch gegeben ist eine Funktion x' * Q * x mit Q positiv definite Matrix. Ich möchte nun wissen welches c_max die Gleichung c_max >= x'*Q*x für alle x Element des Polytops C erfüllt. Also was das größte Elipsoid ist, welches vollständig in C liegt.
Problem/Ansatz:
Mein Ansatz war im 2D folgender:
C = [-2 0; 2 0; 0 -2; 0 2];
%Variable Ellipsoid
Qf = [2, 1; 0, 2];
c = sdpvar(1);
constraints = [C(1,:)*Qf*C(1,:)'>=c, C(2,:)*Qf*C(2,:)'>=c,...
C(3,:)*Qf*C(3,:)'>=c, C(4,:)*Qf*C(4,:)'>=c];
objective = -c;
sol = optimize(constraints, objective);
c = double(c)
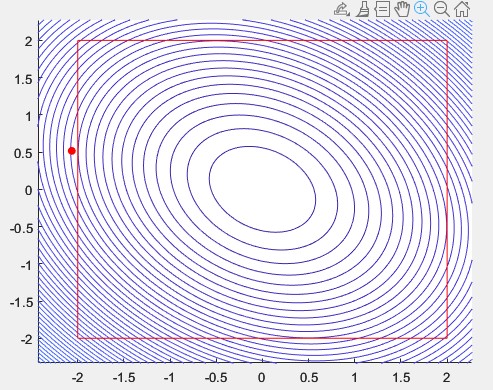
Leider scheitert der Ansatz daran, dass wenn Q Einträge auf den Nebendiagonalen hat, ein c gefunden wird, bei dem c_max >= x'*Q*x auch für x außerhalb von P erfüllt wird. Siehe Bild.
Habt ihr eine Idee wie ich ein c_max bestimmen kann ?