Aufgabe:
Laplace
Problem/Ansatz:
Kann mir jemand sagen was hier vor sich geht?
Wie kommen die in rot eingekreisten Zahlen zustande?
Danke
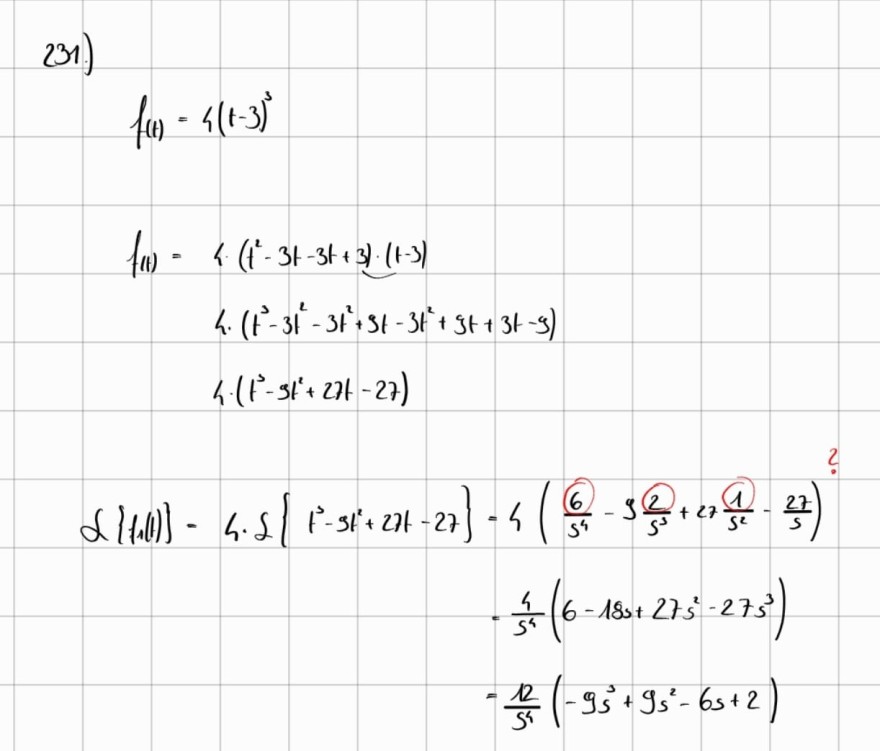
Text erkannt:
231)
\( \begin{aligned} f(t)= & \left\{(t-3)^{3}\right. \\ f(1)= & 4\left(t^{2}-3 t-3 t+3\right) \cdot(t-3) \\ & 4 \cdot\left(t^{3}-3 t^{2}-3 t^{2}+3 t-3 t^{2}+9 t+3 t-9\right) \\ & 4 \cdot\left(t^{3}-5 t^{2}+27 t-27\right) \\ d[t(1)]= & 4 \cdot \delta\left\{t^{3}-s t^{2}+27 t-27\right\}=4\left(\frac{6}{s^{4}}-9 \frac{2}{s^{3}}+27 \frac{1}{s^{2}}-\frac{27}{s}\right) \\ & =\frac{4}{s^{4}}\left(6-18 s+27 s^{2}-27 s^{3}\right) \\ & =\frac{12}{s^{4}}\left(-9 s^{3}+9 s^{2}-6 s+2\right) \end{aligned} \)