Aufgabe:
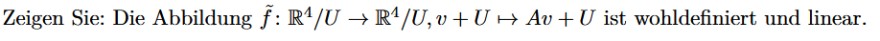
Text erkannt:
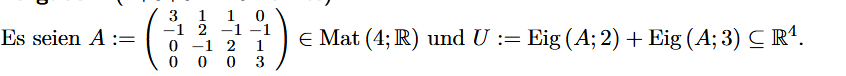
Text erkannt:
Es seien \( A:=\left(\begin{array}{cccc}3 & 1 & 1 & 0 \\ -1 & 2 & -1 & -1 \\ 0 & -1 & 2 & 1 \\ 0 & 0 & 0 & 3\end{array}\right) \in \operatorname{Mat}(4 ; \mathbb{R}) \) und \( U:=\operatorname{Eig}(A ; 2)+\operatorname{Eig}(A ; 3) \subseteq \mathbb{R}^{4} \).
Zeigen Sie: Die Abbildung \( \tilde{f}: \mathbb{R}^{4} / U \rightarrow \mathbb{R}^{4} / U, v+U \mapsto A v+U \) ist wohldefiniert und linear.
Wobei die Basis von $$ \mathbb{R}^{4} / U $$ ist {(1,0,0,0),(0,1,0,0)}
Problem/Ansatz:
Wie genau zeige ich das jetzt? Linear sind ja nur die Bedingungen, aber wohldefiniert weiß ich nicht. Bei der Linearität bin ich mir allerdings auch in diesem Falle sehr unsicher
LInearität Additiv:
Für alle $$v_1 + U, v_2 + U \in \mathbb{R}^4 / U$$ gilt:
$$ \tilde{f}((v_1 + U) + (v_2 + U)) = \tilde{f}(v_1 + v_2 + U) = A(v_1 + v_2) + U = Av_1 + Av_2 + U = (A v_1 + U) + (A v_2 + U) = \tilde{f}(v_1 + U) + \tilde{f}(v_2 + U) $$
Homogenität:
Für alle $$v + U \in \mathbb{R}^4 / U$$ und alle Skalare $c$ gilt:
$$ \tilde{f}(c(v + U)) = \tilde{f}(cv + U) = A(cv) + U = c(Av) + U = c(Av + U) = c \tilde{f}(v + U) $$