Zeigen Sie, dass g: U → ℝ, x \mapsto\|f(x)\|_{2} kein Maximum annimmt.

Question

Aufgabe:

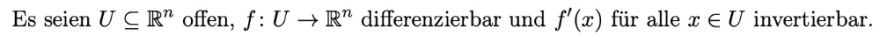
Text erkannt:

Es seien \( U \subseteq \mathbb{R}^{n} \) offen, \( f: U \rightarrow \mathbb{R}^{n} \) differenzierbar und \( f^{\prime}(x) \) für alle \( x \in U \) invertierbar.

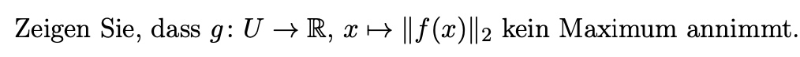
Text erkannt:

Zeigen Sie, dass \( g: U \rightarrow \mathbb{R}, x \mapsto\|f(x)\|_{2} \) kein Maximum annimmt.

Problem/Ansatz:

Wir dachten wir könnten annehmen, dass g ein lokales Maximum an einer Stelle x_0 ∈ U annimmt. Durch die Berechnung der partiellen Ableitungen von g zeigen wir, dass diese nur verschwinden können, wenn f(x_0) = 0 ist. Da f′(x) invertierbar ist, haben die Spalten der Jacobi-Matrix J_f(x_0) lineare Unabhängigkeit, was bedeutet, dass der einzige Vektor, der senkrecht auf allen Spalten steht, der Nullvektor ist. Daher folgt, dass f(x_0) = 0, und somit g(x_0) = ||f(x_0)||_2 = 0. Da dies im Widerspruch zur Annahme eines Maximums steht, kann g kein Maximum in U annehmen?

Der Weg scheint sehr aufwendig wir wissen nicht mehr weiter.

Answer 1

Genau so würde ich es auch machen. Der Einfachheit wegen könnt ihr das auch für die Funktion \( \left\| f( x) \right\|_{2} ^{ 2}\) zeigen, da
diese genau dann ein Maximum hat, wenn \( \left\| f( x) \right\|_{2} \) eines hat. Nun die einzelnen Funktionen ableiten, also zürst \( \left\| x\right\|_{2} ^{ 2}\)
\(\begin{aligned} \left\| x + h\right\|_{2} ^{ 2} = ( x + h) ^{\mathsf{T}}( x + h) = \left\| x\right\|_{2} ^{ 2} + \underbrace{  2x^{\mathsf{T}} h}_{\mathrm{D}\left\| \cdot \right\|_{2} ^{ 2}( x)[h]} + o( h) .\end{aligned}\)
Dann ergibt sich mittels Kettenregel
\(\begin{aligned} \mathrm{D}\left\| f( x) \right\|_{2} ^{ 2}( x) = \mathrm{D}\left\| \cdot \right\|_{2} ^{ 2}( f( x) ) \cdot \mathrm{D}f( x) = 2 f( x) ^{\mathsf{T}} \mathrm{D}f( x) .\end{aligned}\)
Wenn jetzt \( \left\| f( x) \right\|_{2} ^{ 2}\) ein lokales Maximum in \(x _{ 0}\in U\) annimmt, so muss \( \nabla f( x_{ 0} ) = 0\) gelten, also
\(\begin{aligned} \mathrm{D}f( x)^{\mathsf{T}}f( x _{ 0} )  = 0 \end{aligned}\)
was aber nur möglich ist, wenn \( f( x_{ 0} ) = 0\), also würde
\(\begin{aligned} \forall x\in U\colon \left\| f( x) \right\|_{2} ^{ 2}\leqslant 0 \end{aligned}\)
und somit \( f \equiv_{} 0\) gelten, was aber der Invertierbarkeit von \( \mathrm{D}f( x)\) widerspricht.