Berechnen Sie die folgenden Integrale, Partielle Integration

Question

Aufgabe:

Berechnen Sie die folgenden Integrale.

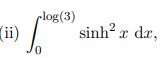
Text erkannt:

(ii) \( \int \limits_{0}^{\log (3)} \sinh ^{2} x \mathrm{~d} x \),

Problem/Ansatz:

Ich mache die Partielle Integration aber da sich sinh und cosh ja nur im Kreis drehen könnte ich das ja ewig machen. Ich sehe da keinen richtigen Ausweg. Ich dachte eventuell an cosh^2(x) − sinh^2(x) = 1. Das Ergebnis soll laut dem Integralrechner 10/9 - log3/2 sein, wie soll man da bitte drauf kommen?

Comments

mit Weg:

https://www.integralrechner.de/

Answer 1

\(sinh(x)=0,5*( e^{x} -e^{-x})\)

\(sinh^2(x)=0,25*( e^{2x} -2+e^{-2x})\)

\( \int\limits_{0}^{log3}0,25*( e^{2x} -2+e^{-2x})dx= 0,25*\int\limits_{0}^{log3}( e^{2x} -2+e^{-2x})dx \)

...

Comments

\( \int\limits_{}^{}e^{2x}dx= \)

Substitution: \(2x=u\)  →\( x=\frac{u}{2} \)  →\(dx=\frac{1}{2}du \)

\( \int\limits_{}^{}e^{2x}dx=\frac{1}{2}*\int\limits_{}^{}e^{u}du \)

Resubstitution:

\( \int\limits_{}^{}e^{2x}dx=\frac{1}{2}*e^{2x}+C \)