In welchen Fällen ist V ein R-Vektorraum?

Question

Aufgabe:

Entscheiden Sie in den folgenden Fällen, ob \( (V,+, \cdot) \) ein \( \mathbb{R} \)-Vektorraum ist.
a) \( V=\mathbb{R}^{2} \) mit der Addition \( \left(\begin{array}{l}v_{1} \\ v_{2}\end{array}\right)+\left(\begin{array}{l}w_{1} \\ w_{2}\end{array}\right):=\left(\begin{array}{l}v_{1}+w_{1} \\ v_{2}+w_{2}\end{array}\right) \) und der Skalarmultiplikation \( \lambda \cdot\left(\begin{array}{l}v_{1} \\ v_{2}\end{array}\right):= \) \( \left(\begin{array}{c}\lambda v_{1} \\ \frac{1}{\lambda} v_{2}\end{array}\right) \), falls \( \lambda \neq 0 \) und \( \lambda \cdot\left(\begin{array}{l}v_{1} \\ v_{2}\end{array}\right):=\left(\begin{array}{l}0 \\ 0\end{array}\right) \), falls \( \lambda=0 \)
b) \( V=\mathbb{R}^{2} \) mit der Addition \( \left(\begin{array}{l}v_{1} \\ v_{2}\end{array}\right)+\left(\begin{array}{c}w_{1} \\ w_{2}\end{array}\right):=\left(\begin{array}{c}v_{1}+w_{1} \\ v_{2} \cdot w_{2}\end{array}\right) \) und der Skalarmultiplikation \( \lambda \cdot\left(\begin{array}{l}v_{1} \\ v_{2}\end{array}\right):= \) \( \left(\begin{array}{c}v_{1} \\ \lambda \cdot v_{2}\end{array}\right) \)
c) \( V=\mathbb{R}^{2} \) mit der Addition \( \left(\begin{array}{l}v_{1} \\ v_{2}\end{array}\right)+\left(\begin{array}{l}w_{1} \\ w_{2}\end{array}\right):=\left(\begin{array}{c}v_{1}+2 \cdot w_{1} \\ v_{2}+w_{2}\end{array}\right) \) und der Skalarmultiplikation \( \lambda \cdot\left(\begin{array}{c}v_{1} \\ v_{2}\end{array}\right):= \) \( \left(\begin{array}{l}\lambda \cdot v_{1} \\ \lambda \cdot v_{2}\end{array}\right) \)

Problem/Ansatz:

Kann mir jemand erklären wie man ein Vektorraum hier beweist und welche davon Vektorräume sind?

Answer 1

a) kein Vektorraum, da \((\lambda+\mu)\cdot v=\lambda\cdot v+\mu\cdot v\) nicht

durchgängig erfüllt. Finde ein Gegenbeispiel.

b) kein Vektorraum. Finde Gegenbeispiel.

c) kein Vektorraum, da Addition nicht assoziativ. Finde Gegenbeispiel.

Comments

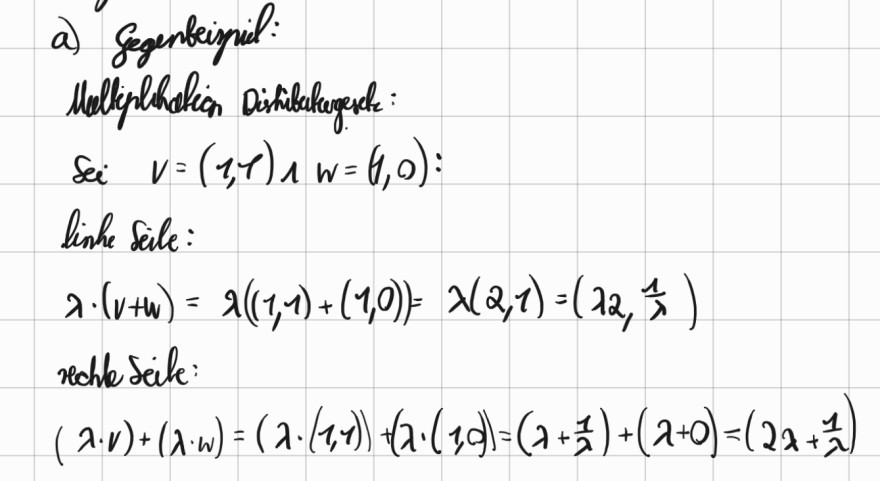
Text erkannt:

a) Gegenbeisuil:
Maltepluhaticin Dishibatugesect:
Si \( v=(1,1) \wedge w=(1,0) \) :
linhe Seile:
\( \lambda \cdot(v+w)=\lambda((1,1)+(1,0))=\lambda(2,1)=\left(\lambda 2, \frac{1}{\lambda}\right) \)
reche deile:
\( (\lambda \cdot v)+(\lambda \cdot w)=(\lambda \cdot(1, y))+(\lambda \cdot(1,0))=\left(\lambda+\frac{1}{\lambda}\right)+(\lambda+0)=\left(2 \lambda+\frac{1}{\lambda}\right) \)

Also ich habe das überprüft bei a) und finde das Gegenbeispiel irgendwie nicht

---

Es geht um das andere Distributivgesetz, so wie ich es angegeben habe.

Wähle \(\lambda=\mu=2\) und \(v={0 \choose 1}\).