Bestimmen Sie die Jordansche Normalform von A mit Kriterien

Question

Aufgabe:

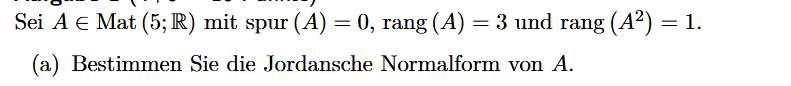
Text erkannt:

Sei \( A \in \operatorname{Mat}(5 ; \mathbb{R}) \) mit spur \( (A)=0, \operatorname{rang}(A)=3 \) und \( \operatorname{rang}\left(A^{2}\right)=1 \)
(a) Bestimmen Sie die Jordansche Normalform von \( A \).

Problem/Ansatz:

Die Spur der JNF muss auch 0 sein. Aber ich finde nichts womit ich irgendwas mit den Infos über den Rang aussagen kann. Auf der Spur der JNF müssen die Eigenwerte stehen.

Ich wäre dankbar um einen Tipp

Comments

Vorschlag: \(J=\left(\!\begin{array}{ccc|cc}0&1&0&0&0\\0&0&1&0&0\\0&0&0&0&0\\\hline0&0&0&0&1\\0&0&0&0&0\end{array}\!\right)\).

---

Ich wäre um einen kleinen Kommentar dazu dankbar wie du dir das überlegt hast :D

---

Ich habs verstanden. EIne Verständnisfrage noch. Wir könnten auch einen Jordanblock machen mit 3 einsen und einen nur mit dem Eigenwert richtig?

---

Meinst du \(J=\left(\!\begin{array}{cccc|c}0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&0\\\hline0&0&0&0&0\end{array}\!\right)\) ?
Das wird nicht funktionieren, weil dann \(\operatorname{rang}(J^2)=2\) ist.

---

Ja genau das meinte ich. Aber in der Aufgabe geht es ja nicht um den Rang von J sondern von A odr impliziert dies, dass der Rang von $$J^2$$auch so sein muss ? Oder sagt der Rang etwas über die größe der Jordanblöcke aus?

---

Die Matrizen \(A\) und \(J\) haben die gleiche JNF. Du kannst davon ausgehen, dass \(A\) bereits in JNF vorliegt.

---

Aber in der Aufgabe geht es ja nicht um den Rang von J sondern von A

Ähnliche Matrizen haben den gleichen Rang.

https://de.m.wikipedia.org/wiki/%C3%84hnlichkeit_(Matrix)

---

Vielen Vielen Dank !