Aufgabe:
Problem/Ansatz:
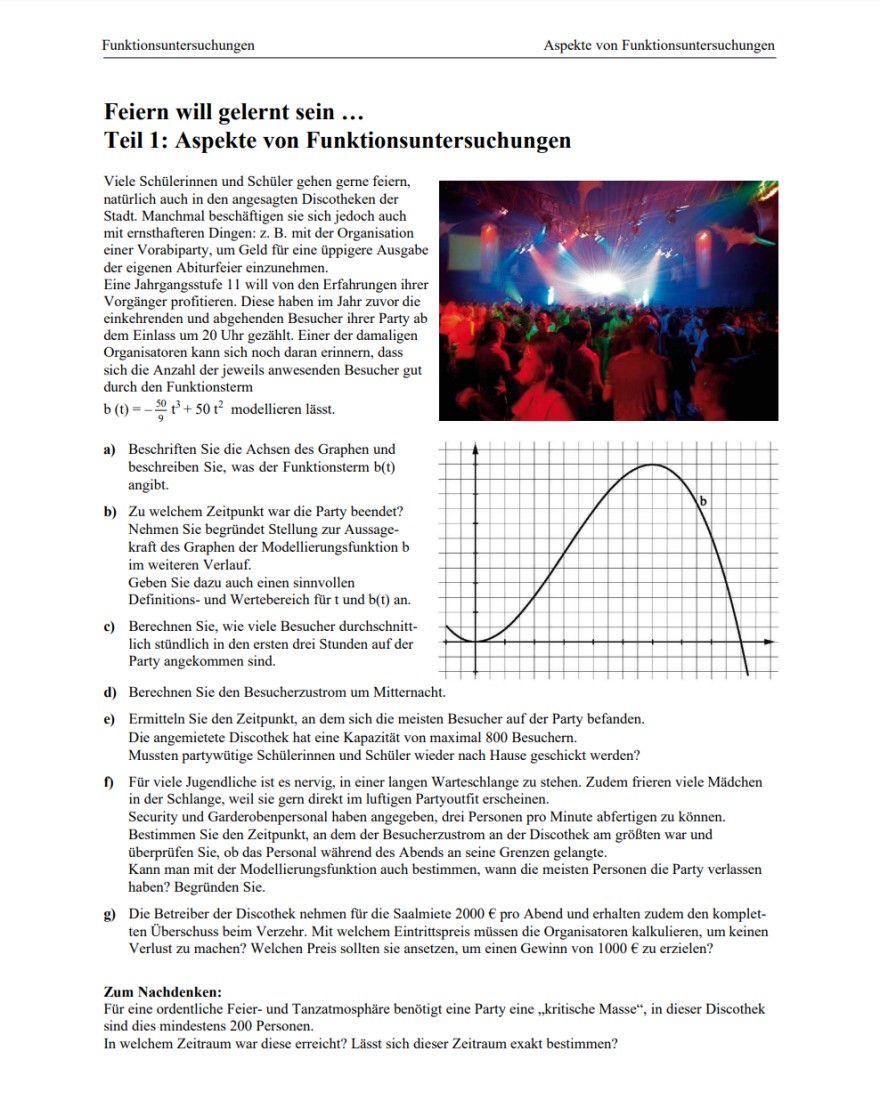
Bei f)
Um den Zeitpunkt zu bestimmen, an dem der Besucherzustrom an der Discothek am größten war, müssen wir die Ableitung des Funktionsterms b(t) bilden und die Ableitung gleich null setzen. Dann überprüfen wir, ob der kritische Punkt ein Maximum oder ein Minimum ist, indem wir die zweite Ableitung berechnen.
Die Ableitung von b(t) ergibt:
b'(t) = d/dt [-(50/9)t^3 + 50t^2]
= -(150/9)t^2 + 100t
Um den kritischen Punkt zu finden, setzen wir die Ableitung gleich null:
0 = -(150/9)t^2 + 100t
Multiplizieren wir diese Gleichung mit 9, um den Bruch zu eliminieren:
0 = -150t^2 + 900t
Nun faktorisieren wir die Gleichung:
0 = 150t(6 - t)
Daraus ergeben sich zwei Lösungen:
t1 = 0
t2 = 6
Der kritische Punkt bei t = 0 wird ausgeschlossen, da es vor dem Einlass liegt. Daher betrachten wir nur den kritischen Punkt bei t = 6.
Um festzustellen, ob es sich um ein Maximum oder ein Minimum handelt, berechnen wir die zweite Ableitung von b(t):
b''(t) = d^2/dt^2 [-(50/9)t^3 + 50t^2]
= -(300/9)t + 100
Setzen wir t = 6 ein:
b''(6) = -(300/9)(6) + 100
= -200 + 100
= -100
Da die zweite Ableitung bei t = 6 negativ ist, handelt es sich um ein Maximum.
Daher war der Besucherzustrom an der Discothek am größten, als t = 6 Stunden.
ist das soweit richtig?