Wie werden diese Art von Rechnung genannt?

Question

Aufgabe:

Wie werden diese Art von Rechnung genannt?

Problem/Ansatz:

Ich habe hier mit meiner Nachhilfe etwas ausgerechnet und möchte nun nochmal wissen, wie man diese Art von Rechnung hier eigentlich nennt?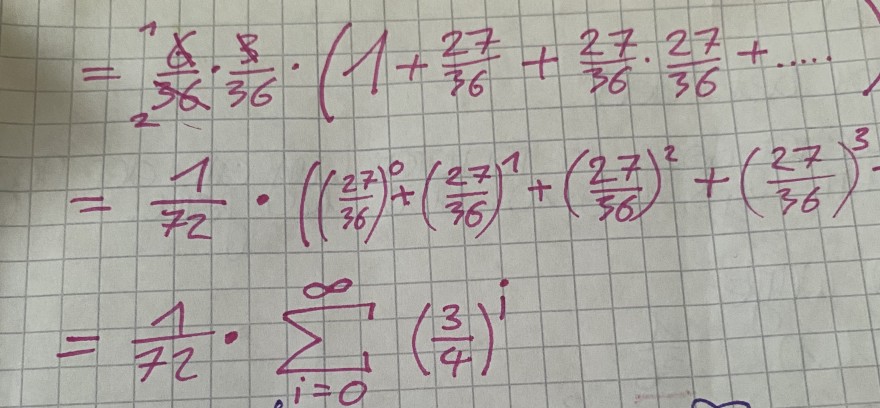

Text erkannt:

\( \begin{array}{l}=\frac{\alpha}{36} \cdot \frac{9}{36} \cdot\left(1+\frac{27}{36}+\frac{27}{36} \cdot \frac{27}{36}+\ldots . .\right. \\ =\frac{1}{72} \cdot\left(\left(\frac{27}{36}\right)^{0}+\left(\frac{27}{36}\right)^{1}+\left(\frac{27}{36}\right)^{2}+\left(\frac{27}{36}\right)^{3}\right. \\ =\frac{1}{72} \cdot \sum \limits_{i=0}^{\infty}\left(\frac{3}{4}\right)^{i}\end{array} \)

Answer 1

Das ist eine geometrische Reihe: q= 27/36

Summenwert 1/72* 1/(1-3/4) = 1/18

Answer 2

Hallo

nach dem Ausklammern ist das die Summe über eine geometrische Reihe, \( \sum\limits_{n=0}^{\infty}{q^n} \) von der man weiß, dass sie  \( \frac{1}{1-q} \) ergibt, wenn q<1 ist. Bei dir q=3/4

Gruß lul

Comments

Ok danke :)

Wofür sind die Schritte vor der geometrischen Reihe wichtig bzw. hätte ich nicht einfach direkt die geometrische Reihe verwenden können?

---

Hallo

die Aufgabe vor deinem Zettel kenn ich ja nicht, aber offensichtlich war das nicht eine Summe über q^n, um die zu sehen musste man offensichtlich erst  die 1/72 ausklammern.

lul