Aufgabe: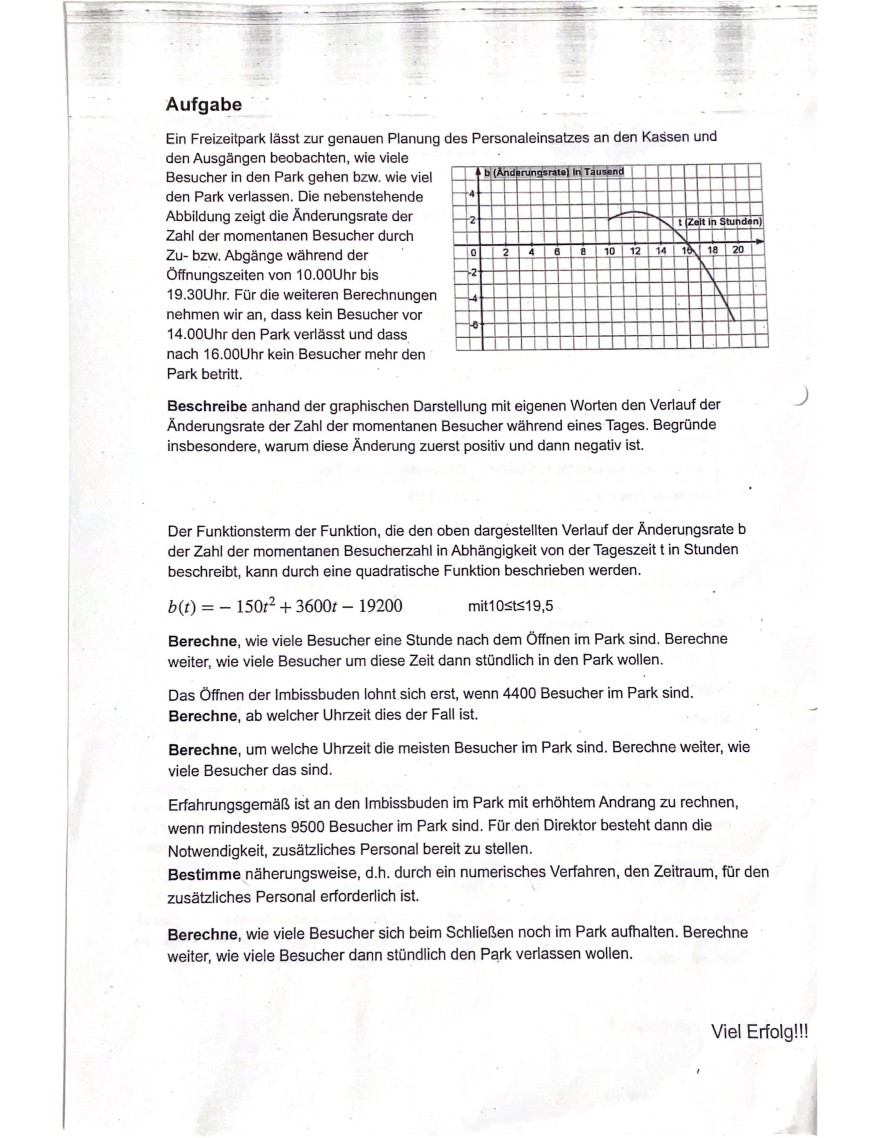
Text erkannt:
Aufgabe
Ein Freizeitpark lässt zur genauen Planung des Personaleinsatzes an den Kasisen und den Ausgängen beobachten, wie viele
Besucher in den Park gehen bzw. wie viel den Park verlassen. Die nebenstehende Abbildung zeigt die Ånderungsrate der Zahl der momentanen Besucher durch Zu- bzw. Abgänge während der Öffnungszeiten von \( 10.00 \mathrm{Uhr} \) bis 19.30Uhr. Für die weiteren Berechnungen nehmen wir an, dass kein Besucher vor 14.00Uhr den Park verlässt und dass nach 16.00Uhr kein Besucher mehr den Park betritt.
Beschreibe anhand der graphischen Darstellung mit eigenen Worten den Verlauf der Ånderungsrate der Zahl der momentanen Besucher während eines Tages. Begründe insbesondere, warum diese Änderung zuerst positiv und dann negativ ist.
Der Funktionsterm der Funktion, die den oben dargestellten Verlauf der Ånderungsrate b der Zahl der momentanen Besucherzahl in Abhängigkeit von der Tageszeit \( \mathrm{t} \) in Stunden beschreibt, kann durch eine quadratische Funktion beschrieben werden.
\( b(t)=-150 t^{2}+3600 t-19200 \quad \) mit \( 10 \leq t \leq 19,5 \)
Berechne, wie viele Besucher eine Stunde nach dem Öffnen im Park sind. Berechne weiter, wie viele Besucher um diese Zeit dann stündlich in den Park wollen.
Das Öffnen der Imbissbuden lohnt sich erst, wenn 4400 Besucher im Park sind. Berechne, ab welcher Uhrzeit dies der Fall ist.
Berechne, um welche Uhrzeit die meisten Besucher im Park sind. Berechne weiter, wie viele Besucher das sind.
Erfahrungsgemäß ist an den Imbissbuden im Park mit erhöhtem Andrang zu rechnen, wenn mindestens 9500 Besucher im Park sind. Für den Direktor besteht dann die Notwendigkeit, zusätzliches Personal bereit zu stellen.
Bestimme näherungsweise, d.h. durch ein numerisches Verfahren, den Zeitraum, für den zusätzliches Personal erforderlich ist.
Berechne, wie viele Besucher sich beim Schließen noch im Park aufhalten. Berechne weiter, wie viele Besucher dann stündlich den Park verlassen wollen.
Viel Erfolg!!!
Ich brauche Hilfe bei der Lösung dieser Aufgaben.
…
Problem/Ansatz: