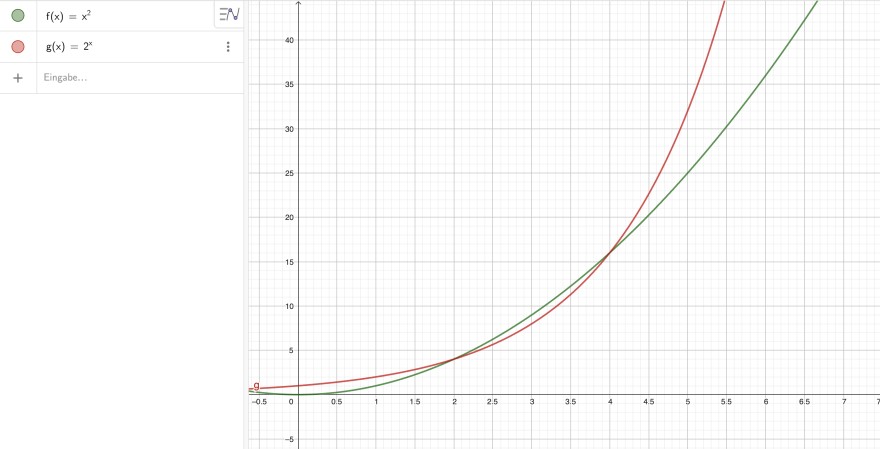
Bei solchen Aufgaben hilft es immer wieder mal sich die Funktionen zeichnen zu lassen. Für die beiden Funktionen \( f(n) = n² \) und \( g(n) = 2^{n} \) sieht das so aus:
Jetzt müssen wir uns die Definitionen der einzelnen Symbole anschauen:
\( f \in O(g) \) bedeutet, dass f unter g liegt.
\(f \in Ω(g) ⇔ g \in O(f) \) ersteres bedeutet f liegt über g, das heißt automatisch, dass g unter f liegen muss.
\( f \in Θ(g) ⇔f \in O(g) ∧ f \in Ω(g)\)
\( f \in o(g) ⇔ \lim\limits_{n\to\infty} \frac{f(n)}{g(n)} = 0\), das heißt g wächst schneller als f.
\( f \in ω(g) ⇔ \lim\limits_{n\to\infty} \frac{f(n)}{g(n)} = \infty\), das heißt f wächst schneller als g.
Zur Lösung:
\( f \in O(g) \) gilt schonmal, da ab ca. n = 4 die Funktion \( f \) definitiv unter \( g \) liegt.
\( f \notin Ω(g)\) da f nur in einem kleinen Intervall ( \( [2,3; 4)\)) über g liegt, dann aber wieder darunter!
\( f \in o(g) \) da g wesentlich schneller wächst als f. Dazu kann man sich einfach folgenden Grenzwert anschauen:
\( \lim\limits_{n\to\infty} \frac{f(n)}{g(n)} = \lim\limits_{n\to\infty} \frac{n²}{2^{n}} = 0\) da eine Exponentialfunktion immer schneller wächst als eine quadratische Funktion!
\( f \notin Θ(g) \) da dafür \( f \in O(g) \) und \( f \in Ω(g)\) gelten müsste!
und \( f \in ω(g) \) kann ebenfalls nicht gelten, da ja schon \( f \in o(g) \) gilt. Das heißt wenn g schneller wächst als f, kann nicht auch f schneller als g wachsen. Das heißt \( f \notin ω(g) \)
PS: Ich weiß die Antwort kam spät, aber vielleicht hilft sie in Zukunft anderen Studierenden!