Fourier Reihen cos(0)?

Question

Aufgabe

Hallo! Kurze Frage zu Fourier Reihen-

Problem/Ansatz:

Wie kommt man hier bei a0 auf cos(0)?  Also woher kommt die Null :D

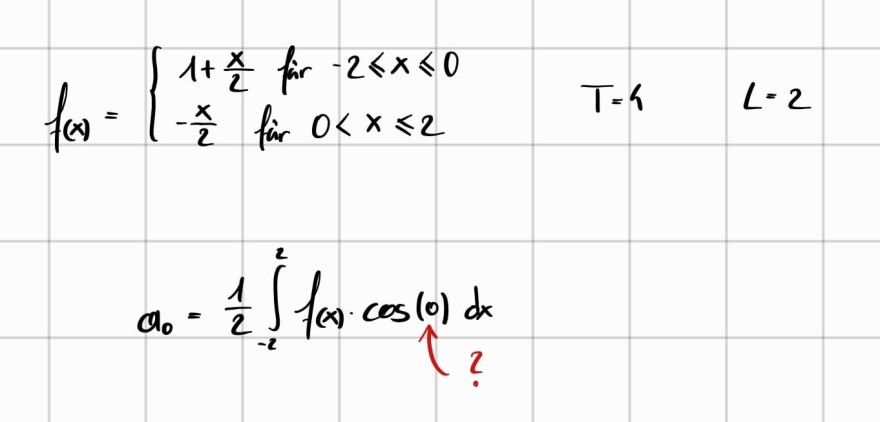
Text erkannt:

\( \begin{array}{l} f(x)=\left\{\begin{array}{l}1+\frac{x}{2} \text { für }-2 \leqslant x \leqslant 0 \\ -\frac{x}{2} \text { für } 0<x \leqslant 2\end{array} \quad T=1 \quad<-2\right. \\ a_{0}=\frac{1}{2} \int \limits_{-2}^{2} f(x) \cdot \cos (0) d x\end{array} \)

Answer 1

Hallo so sind die ak definiert

$$a_{{k}} = {\frac{1}{2 }}\int _{{-2 }}^{{2 }}f(t)\cdot \cos \left(kt\right){\mathrm d}t\quad {\text{für }}k\geq 0$$

jetzt setze k=0

lul