Berechnet werden soll der Konvergenzradius der Reihe.

Question

Aufgabe:

Berechnet werden soll der Konvergenzradius der Reihe:

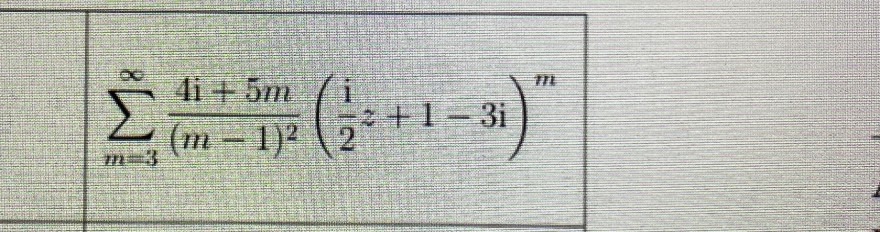
Text erkannt:

\( \sum \limits_{m=3}^{\infty} \frac{4 \mathrm{i}+5 m}{(m-1)^{2}}\left(\frac{\mathrm{i}}{2} z+1-3 \mathrm{i}\right)^{m} \)

Soweit, so gut.

Habe auch ein bisschen rumgerechnet und komme auf einen Konvergenzradius von r=1. Wolframalpha bestätigt das Ergebnis auch. In der Lösung zur Aufgabe kommen sie allerdings auf r=2 und ich weiß beim besten Willen nicht wie.

Macht der Startwert von m=3 der Reihe einen Unterschied?

Vielleicht mag es ja jemand durchrechnen und mir schnell Rückmeldung geben. Vielen Dank!

Comments

Wie hast Du denn gerechnet?

---

Also mit Cauchy-Hadamard habe ich nur ein bisschen rumprobiert aber mit der Methode die dem Quotientenkriterium ähnelt bin ich recht schnell auf 1 gekommen. Finde gerade meinen Aufschrieb nicht aber man kann da ja recht schön rumkürzen (größte Potenz ausklammern und so) und da blieb halt nur 1 übrig. Jetzt hab ich allerdings nicht überprüft, ob das Kriterium hier überhaupt anwendbar ist...

Ich will eigentlich nur wissen, ob ich mich einfach verrechnet habe oder, ob die Lösung (r=2) einfach falsch ist.

---

Hallo

der Radius 1 wäre richtig, für z^m aber du hast ja die Klammer^m also was bedeutet das für |z|?

lul

---

Aber ist die Form nicht standardmäßig a_m *(z-z_o)^m?

---

Ah also muss man erst * (i/2)^m *(2/i)^m (also effektiv * 1) machen, damit man auf die Form (z-z₀)^m kommt?

Joa dann sehe ich schon eher wie da 2 rauskommt. Vielen Dank schon mal!