lokalen Extrema der Funktion bestimmen

Question

Aufgabe:

Text erkannt:

Aufgabe 3 (Lokale Extrema).
(14 Punkte)
Bestimmen Sie alle lokalen Extrema der Funktion \( f:[0,1] \rightarrow \mathbb{R}, f(x):=\sqrt{x}+\sqrt{4-2 x} \).
(Dazu gehört die Bestimmung der Extremstellen, -werte und Arten der Extrema).

Problem/Ansatz:

Hallo Leute,

ich scheiter gerade an dieser Aufgabe. Ich habe Schwierigkeiten f '(x) = 0 auszurechen.

Es wäre super Hilfreich, wenn mir jemand die notwendige Bedingung bezüglich dieser Aufgabe erläutern würde!

Vielen Dank!!

Answer 1

\(\begin{aligned} &  & f(x) & =\sqrt{x}+\sqrt{4-2x}\\ & \implies & f(x) & =x^{\frac{1}{2}}+\left(4-2x\right)^{\frac{1}{2}}\\ & \implies & f'(x) & =\frac{1}{2}x^{-\frac{1}{2}}+\frac{1}{2}\left(4-2x\right)^{-\frac{1}{2}}\cdot\left(-2\right)\\ &  &  & =\frac{1}{2}x^{-\frac{1}{2}}-\left(4-2x\right)^{-\frac{1}{2}}\\ \\ &  & f'(x) & =0\\ & \iff & 0 & =\frac{1}{2}x^{-\frac{1}{2}}-\left(4-2x\right)^{-\frac{1}{2}}\\ & \iff & 0 & =\frac{1}{2x^{\frac{1}{2}}}-\frac{1}{\left(4-2x\right)^{\frac{1}{2}}}\\ & \iff & 0 & =\frac{\left(4-2x\right)^{\frac{1}{2}}-2x^{\frac{1}{2}}}{2x^{\frac{1}{2}}\left(4-2x\right)^{\frac{1}{2}}}\\ & \iff & 0 & =\left(4-2x\right)^{\frac{1}{2}}-2x^{\frac{1}{2}}\wedge x\neq0\wedge4-2x\neq0\\ & \iff & 2x^{\frac{1}{2}} & =\left(4-2x\right)^{\frac{1}{2}}\wedge x\neq0\wedge4-2x\neq0\\ & \iff & 4x & =4-2x\wedge x>0\wedge4-2x>0\\ & \iff & x & =\frac{2}{3} \end{aligned}\)

Answer 2

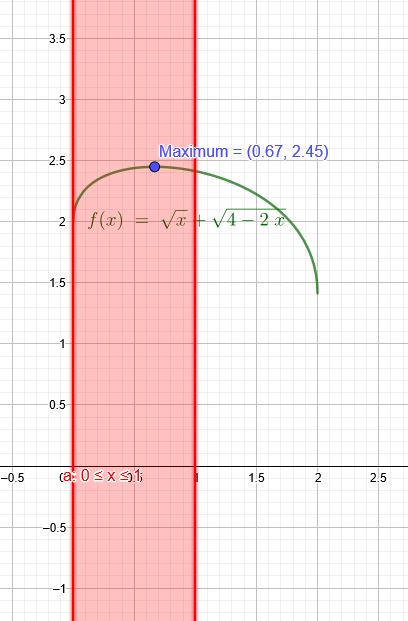
\( f:[0,1] \rightarrow \mathbb{R}, f(x):=\sqrt{x}+\sqrt{4-2 x} \)

\(f´(x)= \frac{1}{2*\sqrt{x}} +\frac{-2}{2*\sqrt{4-2x}}=\frac{1}{2*\sqrt{x}} -\frac{1}{\sqrt{4-2x}}\)

\(\frac{1}{2*\sqrt{x}} -\frac{1}{\sqrt{4-2x}}=0\)

\(\frac{1}{2*\sqrt{x}} =\frac{1}{\sqrt{4-2x}}    |*2*\sqrt{x}\)

\(1=\frac{2*\sqrt{x}}{\sqrt{4-2x}}   |*\sqrt{4-2x}  \)

\(\sqrt{4-2x} =2*\sqrt{x}   | ^{2}\)

\(4-2x =4x \)

\(x=\frac{2}{3} \)   ist ∈ \([0,1]\)    \(  f(\frac{2}{3} )=\sqrt{\frac{2}{3}}+\sqrt{4-2*\frac{2}{3}} =\sqrt{6}≈2,45\)

Art des Extremwertes:

\(f´(x)=\frac{1}{2*\sqrt{x}} -\frac{1}{\sqrt{4-2x}}\)

Bestimme nun die 2.Ableitung

 \(f´´(\frac{2}{3})=a\)  Ist \(a >0\) so liegt ein Minimum vor,wenn \(a <0\) ist es ein Maximum.