Zeigen Sie, dass f genau dann stetig ist, wenn...

Question

Aufgabe:

Hallo

Ich brauche Hilfe beim Beweis der Äquivalenz folgender Aussagen.

Vorab die ganze Aufgabe:

Sei f : X --->Y eine Abbildung zwischen metrischen Räumen (X,d_x  ) und (Y,d_y ). Zeigen Sie, dass f genau dann stetig ist, wenn

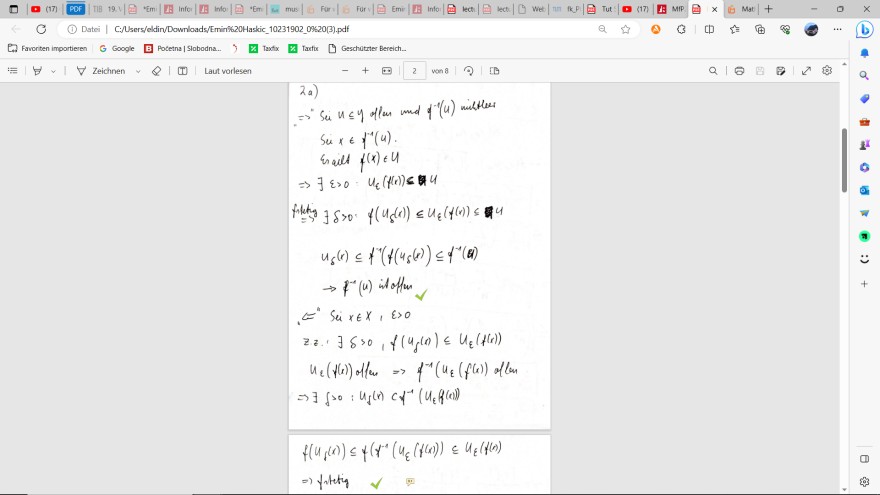
a) für jede offene Menge U ⊆ Y ist das Urbild f^-1  (U) ⊆ X offen

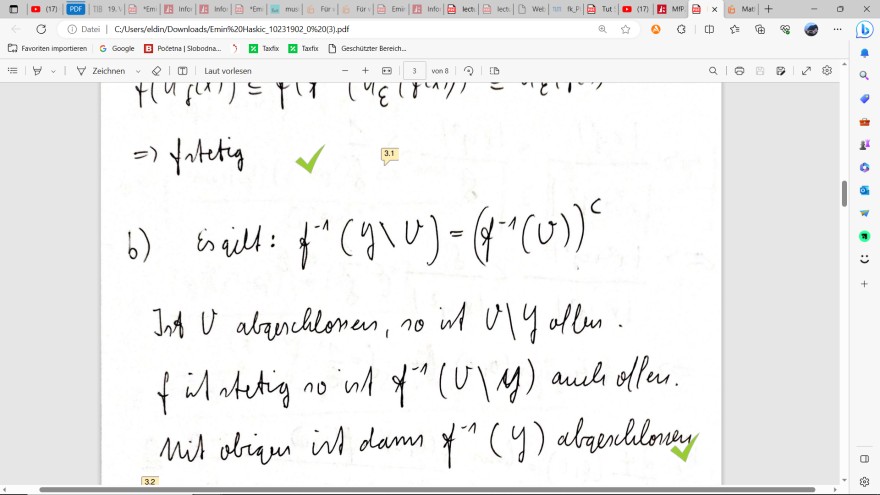
b) für jede geschlossene Menge V ⊆ Y ist das Urbild f^-1  (V) ⊆ X auch geschlossen.

Hinweis: Um Äquivalenz zu zeigen, überlegen Sie sich, was ist f^-1 (Y \ U)

Wie gesagt mir dem Beweis der Äquivalenz komme ich nicht wirklich klar und wäre für jegliche Tipps sehr dankbar...

Lösung zu a) und b) habe ich hochgeladen

Problem/Ansatz:

Comments

Ist das Deine Lösung, die wir prüfen sollen? Oder ist das eine fremde Lösung, die Du nicht verstehst?

---

das ist meine Lösung zu Teilaufgabe a) und b) , die auch richtig sind.

Wir sollen aber noch zeigen, dass bei a) und b) eine Äquivalenz herrscht.

Als Hinweis soll man überlegen was f^-1 (Y\U) ist.

---

Verstehe ich nicht. Du hast doch für a) beide Schluss- Richtungen gezeigt. Das ist doch Äqiuvalenz.

---

Man soll noch zeigen, dass aus der Behauptung b) die Behauptung a) folgt

---

Das ist doch mit Deinem Text zu b) erledigt:

Wenn \(V \sub Y\) abgeschlossen ist, dann ist \(Y \setminus V\) offen, also auch \(f^{-1}(Y \setminus V)=X\setminus f^{-1}(V)\). Daher ist \(f^{-1}(V)\)abgeschlossen:

Umgekehrt genauso.

---

Mein Tutor meint es ist immer noch nicht aussreichend...bin echt am verzweifeln