Gerade g durch den Kugelmittelpunkt senkrecht zu E
g: X = [-1, -8, 4] + r·[2, -1, -2] = [2·r - 1, -r - 8, 4 - 2·r]
Schnitt von g und E
2·(2·r - 1) - (-r - 8) - 2·(4 - 2·r) = -11 → r = -1
Schnitt von g und K
((2·r - 1) + 1)^2 + ((-r - 8) + 8)^2 + ((4 - 2·r) - 4)^2 = 9^2 → r = -3 ∨ r = 3
Mittelpunkt der Kugel bei r = 1
X = [-1, -8, 4] + 1·[2, -1, -2] = [1, -9, 2]
Radius der Kugel
2·|[2, -1, -2]| = 6
Kugelgleichung
Kmax: (x - 1)^2 + (y + 9)^2 + (z - 2)^2 = 6^2
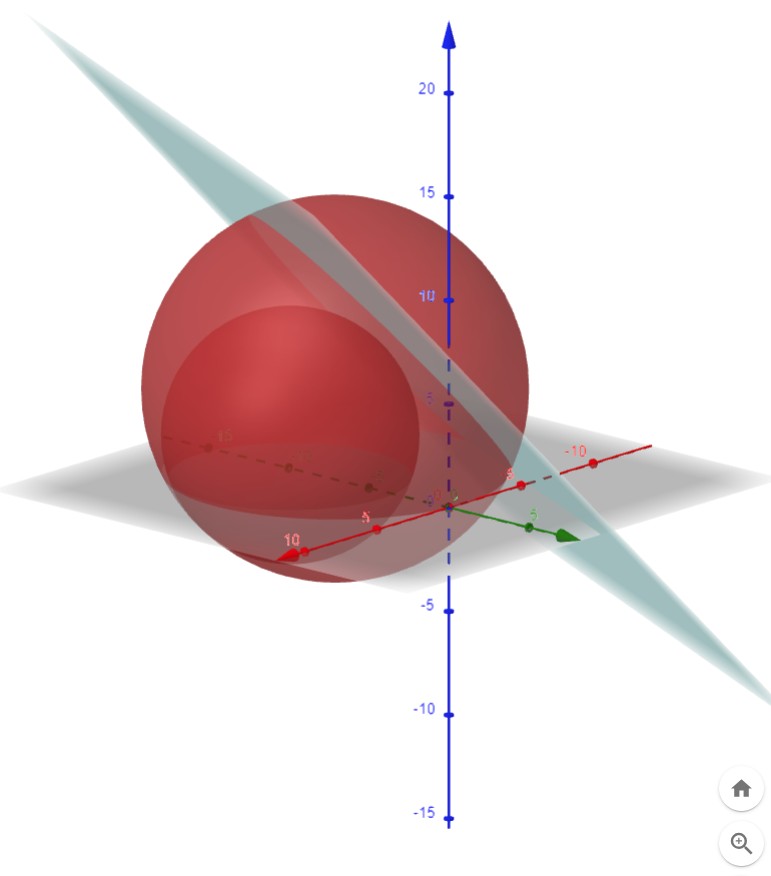
Skizze