Aufgabe:
Was ist der Unterschied zwischen aji und amn ?
Problem/Ansatz:

Text erkannt:
Definition einer Matrix
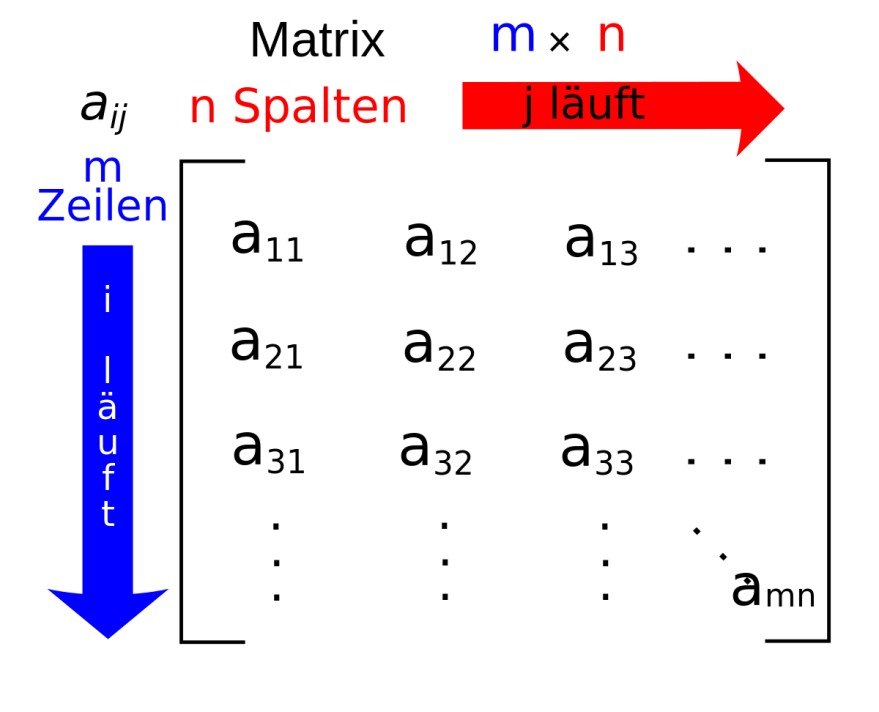
Ein Zahlenschema aus \( \boldsymbol{m} \) Zeilen und \( \mathbf{n} \) Spalten \( \left(m, n \in \mathbb{N}^{*}\right) \) nennt man eine Matrix vom Format \( (m ; n) \) bzw. vom Typ \( (m ; n) \).
Matrizen werden mit großen Buchstaben bezeichnet: A, B, C, ...
\( A=\left(\begin{array}{ccccc} a_{11} & a_{12} & a_{13} & \ldots & a_{1 n} \\ a_{21} & a_{22} & a_{23} & \ldots & a_{2 n} \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ a_{m 1} & a_{m 2} & a_{m 3} & \ldots & a_{m n} \end{array}\right)=\left(a_{1 j}\right)_{m n} \text { mit } i=1, \ldots, m \text { und } j=1, \ldots, n \)
Die Zahlen \( a_{i j} \) heißen Elemente von A. i ist der Zeilenindex; j ist der Spaltenindex. Eine Matrix mit einer Zeile nennt man Zeilenvektor, mit einer Spalte Spaltenvektor. Schreibweise von Vektoren mit Kleinbuchstaben: \( \vec{a}=\left(\begin{array}{llll}15 & 10 & 8 & 7\end{array}\right) \) oder \( \vec{b}=\left(\begin{array}{c}15 \\ 12 \\ 2\end{array} \mid\right. \). Transponierte Vektoren: \( \vec{a}^{\top}=\left(\begin{array}{c}15 \\ 10 \\ 8 \\ 7\end{array}\right) \) oder \( \vec{b}^{\top}=\left(\begin{array}{lll}15 & 12 & 2\end{array}\right) \)