Kreiskegelstumpf: Radien r und R verhalten sich wie 2:1. Berechne die Höhe des Kegelstumpfes.

Question

Bei einem geraden Kegelstumpf verhalten sich die Radien r und R  wie 2:1. Der Neigungswinkel der Mantellinie gegenüber der Grundflache betragt 60°. Berechne die Höhe des Kegelstumpfes.

Answer 1

Diese Angaben genügen nicht zur eindeutigen Bestimmung der Höhe. Es gibt beliebig viele verschieden hohe Kegelstümpfe, für die die Beschreibung zutrifft.

Man kann daher die gesuchte Höhe nur in Abhängigkeit von einem der Radien darstellen. Dazu zunächst eine Skizze:

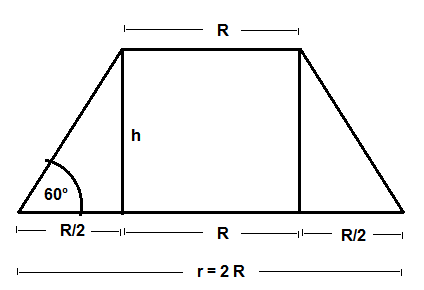
Gezeigt wird ein Schnitt durch einen geraden Kegelstumpf.  Dieser Schnitt ist ein gleichschenkliges Trapez.

Wenn der obere Radius R und der untere Radius r = 2 R ist (das folgt aus r : R = 2 : 1 ), dann ergeben sich die in der Skizze angegebenen Streckenlängen.
Für die Höhe h gilt also in Abhängigkeit vom oberen Radius R offenbar:

h / ( R / 2 ) = tan ( 60 ° )

<=> h = ( R / 2 ) * tan ( 60 ° )

Mit dieser Formel kann man für jedes beliebige R die Höhe eines Kegelstumpfes berechnen, der den Vorgaben der Aufgabenstellung entspricht.

So ergibt sich etwa für R = 5 cm :

h = 2,5 * tan ( 60 ° ) ≈ 4,3 cm