Text erkannt:
Saklierung
Frage 7 von 13 (2 Punkte)
Nicht beantwortet
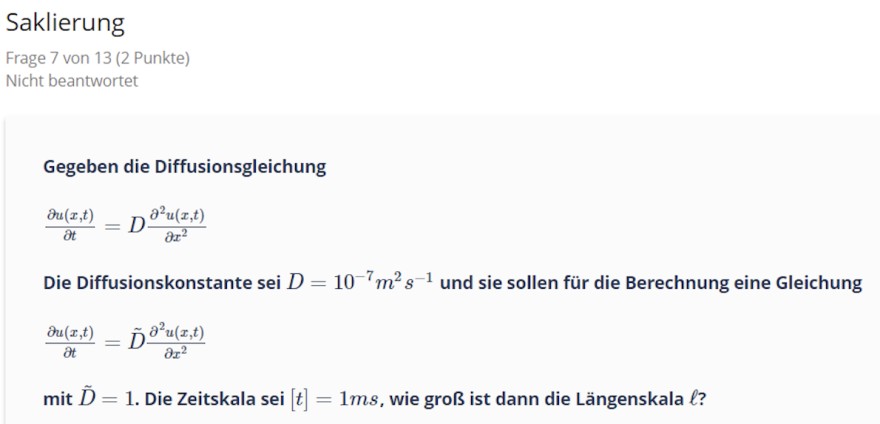
Gegeben die Diffusionsgleichung
\( \frac{\partial u(x, t)}{\partial t}=D \frac{\partial^{2} u(x, t)}{\partial x^{2}} \)
Die Diffusionskonstante sei \( D=10^{-7} \mathrm{~m}^{2} \mathrm{~s}^{-1} \) und sie sollen für die Berechnung eine Gleichung \( \frac{\partial u(x, t)}{\partial t}=\tilde{D} \frac{\partial^{2} u(x, t)}{\partial x^{2}} \)
mit \( \tilde{D}=1 \). Die Zeitskala sei \( [t]=1 \mathrm{~ms} \), wie groß ist dann die Längenskala \( \ell \) ?
Text erkannt:
Methode der Charakteristiken
Frage 2 von 13 (1 Punkt)
Nicht beantwortet
Gegeben sei die partielle Differentialgleichung erster Ordnung folgender Gestalt
\( \frac{\partial f(x(t), v(t), t)}{\partial t}+v(t) \frac{\partial f(x(t), v(t), t)}{\partial x}+\frac{F(x(t))}{m} \frac{\partial f(x(t), v(t), t)}{\partial v}=\frac{f^{e q}-f(x(t), v(t), t)}{\tau} \)
Welche Art Gleichungen erhalten Sie bei Anwendung der Methode der Charakteristiken!
Aufgabe:
Problem/Ansatz:
Hallo, könnte mir hier jmd. weiterhelfen? Wie ich genau vorgehen muss?
