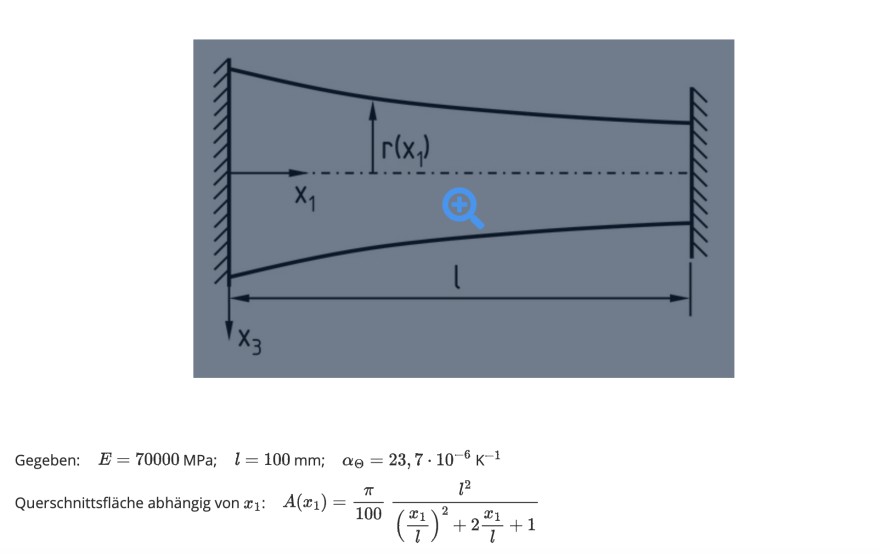
Aufgabe: Hi! ich hab eine Verständnisfrage. In der im Bild gezeigten Aufgabe wird nach der im Balken durch die Temperaturerhöhung ∆Θ = 90K bewirkte Normalkraft gefragt.
Text erkannt:
Gegeben: \( \quad E=70000 \mathrm{MPa} ; \quad l=100 \mathrm{~mm} ; \quad \alpha_{\Theta}=23,7 \cdot 10^{-6} \mathrm{~K}^{-1} \)
Querschnittsfläche abhängig von \( x_{1}: \quad A\left(x_{1}\right)=\frac{\pi}{100} \frac{l^{2}}{\left(\frac{x_{1}}{l}\right)^{2}+2 \frac{x_{1}}{l}+1} \)
Problem/Ansatz:
Der Ansatz ist mir klar:
ε(x) = \( \frac{N}{E*A} \)+α*∆Θ...
Dann stellt man den ganzen spass um und landet bei
N = (-α*∆Θ*E)/Integral(1/A(x))dx) von 0->L
Meine Frage ist eher warum man über die Querschnittsfläche A in Abhängigkeit von x integriert?
Bzw. was man dann erhält... die Gesamtquerschnittsfläche? Die Summe aller Teilquerschnittsflächen? Die Durchschnittquerschnittsfläche? Und was mir das denn anschaulich für die Kraft bringen soll.
Schon mal vorab danke für jegliche Erklärugen :)