Text erkannt:
Es seien
\( w_{1}=\left(\begin{array}{l} 0 \\ 1 \\ 1 \end{array}\right), w_{2}=\left(\begin{array}{c} 0 \\ -1 \\ 1 \end{array}\right), w_{3}=\left(\begin{array}{l} 4 \\ 1 \\ 0 \end{array}\right) . \)
a) Erstellen Sie aus der Basis \( \left(w_{1}, w_{2}, w_{3}\right) \) (des \( \left.\mathbb{R}^{3}\right) \) mit Hilfe des Gram-Schmidt Algorithmus eine Orthonormalbasis (ONB) \( \left(v_{1}, v_{2}, v_{3}\right) \). Beachten Sie dabei, dass \( w_{1}, w_{2} \) bereits orthogonal sind.
Aufgabe:

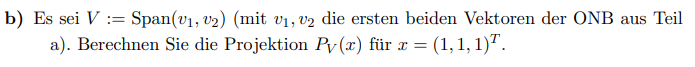
Problem/Ansatz:
Hallo, ich bräuchte hierfür Hilfe. Habe eine kleine Verständnisfrage für die a). Gehört sozusagen der Koeffizient zu z.B. v1?
Wäre also v1 = 1/\( \sqrt{2} \) * \( \begin{pmatrix} 0\\1\\1 \end{pmatrix} \) oder eher nur \( \begin{pmatrix} 0\\1\\1 \end{pmatrix} \)
Und ist meine ONB richtig?
ONB = {1/\( \sqrt{2} \) * \( \begin{pmatrix} 0\\1\\1 \end{pmatrix} \) , 1/\( \sqrt{2} \) * \( \begin{pmatrix} 0\\-1\\1 \end{pmatrix} \) , 1/4 * \( \begin{pmatrix} 4\\0\\0 \end{pmatrix} \)
Zu der b), wegen meiner Verständnisfrage, bin ich mir nicht sicher, mit welchen Vektoren ich arbeiten soll, also ob ein Koeffizient davor ist oder nicht. Desweiteren bin ich mir auch nicht sicher, wie man die Projektion berechnet, da ein Span gegeben ist. Ich weiß, dass ein Span(v1, v2) = s*v1 + t*v2 bedeutet. Weiß aber nicht, was ich damit machen könnte.
Vielen Dank für jegliche Hilfe oder Ansätze.