Orthogonalprojektion Beweis. V=R^2 und U=span(e1). ... weisen Sie nach, dass v-u auf U senkrecht steht.

Question

Aufgabe:

Sei \( V \) ein \( n \) -dimensionaler \( R \) -Vektorraum mit Skalarprodukt und U sein Vektorraum von \( V \). Dann gibt es zu jedem \( v ∈ V \) genau ein \( u ∈ U \), sodass v-u auf allen Vektoren aus U senkrecht steht. Man nennt u Orthogonalprojektion von v auf \( U \)

b) Es sei weiterhin \( V=R^{2} \) und \( U=\left\langle e_{1}\right\rangle . \) Geben Sie den Vektor u für einen beliebigen Vektor \( v \in R^{2} \) an und weisen Sie nach, dass \( v-u \) auf \( U \) senkrecht steht.

Answer 1

Anscheindend wird der Satz vorausgesetzt und du sollst das Beispiel b) bearbeiten.

 V=R² und U=span(e1). ... weisen Sie nach, dass v-u auf U senkrecht steht.

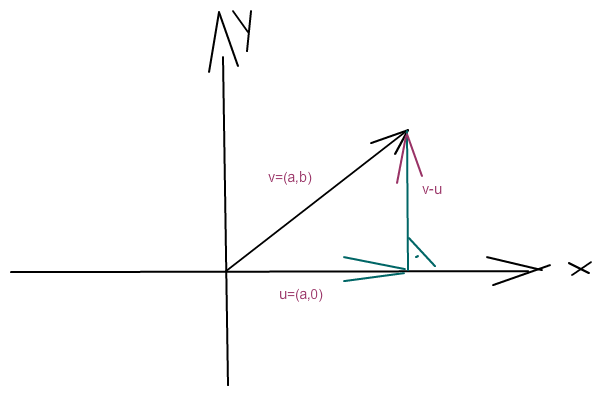
b) Sei v = (a,b) ein beliebiger Vektor in R^2

Dann ist u=(a,0) ein Vektor in U, da (a,0) = a*e1.

Und v-u =(a,b)-(a,0) = (0,b) 

(0,b) steht senkrecht auf (a,0), da das Skalarprodukt (0,b) * (a,0) = 0*a + b*0 = 0

u=(a,0) ist also der gesuchte Vektor. Die sog. Orthogonalprojektion von v auf die x-Achse. Das kannst du zeichnerisch ganz einfach nachvollziehen.