Bestimme die Parametergleichung für die Ebene

Question

Aufgabe:

Im Bild ist das Pultdach eines Hauses zu sehen. Die im Foto sichtbare Dachfläche liegt in einer Ebene, zu der in einem räumlichen Koordinatensystem der Punkt A(0|9|4) und die Richtungsvektoren \( \vec{u} \) =\( \begin{pmatrix} 0\\-2\\0 \end{pmatrix} \) und \( \vec{v} \)=\( \begin{pmatrix} -2\\0\\2 \end{pmatrix} \).

Alle Angaben in Metern. Die Dachfläche ist 7 mal 9 m

a) Bestimme die Parametergleichung für die Ebene.

B) Man kann alle Punkte der Ebene beschreiben, indem man die Parameter für die Ebene einschränkt. Führen Sie dies durch.

C) Geben Sie die Koordinaten aller Eckpunkte der Dachfläche an.

Problem/Ansatz

a)  E: \( \begin{pmatrix} x\\y\\z \end{pmatrix} \)=\( \begin{pmatrix} 0\\9\\4 \end{pmatrix} \)+r·\( \begin{pmatrix} 0\\-2\\0 \end{pmatrix} \)+s·\( \begin{pmatrix} -2\\0\\2 \end{pmatrix} \).

b) r=4,5 s= 2,475

Wie funktioniert c? Ich finde leider überhaupt keinen Ansatz dafür.

Vielen Dank!

Comments

Ergeht um die grüne Ebene. Meine Idee wäre vielleicht die Geraden zu finden, welche die Ebene begrenzen und deren Schnittpunkt zu bestimmen aber wie finde ich die geraden?

---

Dein Ansatz für eine Parametergleichung kann kein valabler Ansatz sein, weil es keine Gleichung ist.

Nachtrag: Roland hat es korrigiert, jetzt ist es eine Gleichung.

Nachtrag 2: Mein diesbezüglicher Hinweis wurde von einem chinesischen Eierdieb getilgt.

---

Die im Foto sichtbare Dachfläche ...

Ist auf dem Foto der Punkt \(A\) zu sehen?

Falls ja - liegt er auf der Ecke des Daches rechts unten wie hier gezeigt?

(klick drauf!)

Answer 1

Wenn man annimmt, dass A ein Eckpunkt der Dachfläche ist, dann ist                  \( \vec{OB} \)=\( \begin{pmatrix} 0\\9\\4 \end{pmatrix} \)+\( \frac{7}{2} \) ·\( \begin{pmatrix} 0\\-2\\0 \end{pmatrix} \) und deshalb B(0|2|4). Wenn man annimmt, dass A ein Eckpunkt der Dachfläche ist, dann ist \( \vec{OC} \)=\( \begin{pmatrix} 0\\9\\4 \end{pmatrix} \)+\( \frac{9}{2·\sqrt{2}} \) ·\( \begin{pmatrix} -2\\0\\2 \end{pmatrix} \) und deshalb       C(-\( \frac{9}{\sqrt{2}} \) | 9 |4+\( \frac{9}{\sqrt{2}} \) ).

Comments

Danke aber wieso kann angenommen werden, dass A ein eckpunkt ist und woher kommen die Zahlen der Parameter?

---

In der originalen Abbildung sind bestimmt noch mehr Informationen gegeben als in deinem vermutlich mit Paint erstellten Kunstwerk.

;-)

---

Die Annahme, dass A ein Eckpunkt ist, stammt von mir.

Die Zahlen der Parameter sind nur dann zutreffend, wenn \( \vec{u} \) und \( \vec{v} \) genau auf den Dachkanten liegen. Solange man über A sowie über \( \vec{u} \) und \( \vec{v} \) nichts weiß, kann man diese Aufgabe nicht lösen.

Answer 2

a) ist richtig. Man schreibt einfacher auch

$$E: \overrightarrow x = \begin{pmatrix} 0\\9\\4 \end{pmatrix} + r \cdot \begin{pmatrix} 0\\-2\\0 \end{pmatrix} + s \cdot \begin{pmatrix} -2\\0\\-2 \end{pmatrix}$$

b) und c) lassen sich so anhand der ungenauen Skizze nicht beantworten.

Da solltest du optimaler Weise die original Aufgabenstellung inkl. Skizze angeben.

Answer 3

Du musst einsetzen:

r=0 und s=0 ;

r=0 und s≈2,475;

r=4,5 und s=0;

r=4,5 und s≈2,475

:-)

Answer 4

Wir nehmen mal an A sei die rechte untere Ecke des Pultdaches. Dann Könnten die Eckpunkte sein

A = [0, 9, 4]

B = [0, 9, 4] + 7/|[-2, 0, 2]|·[-2, 0, 2] = [- 7/2·√2, 9, 7/2·√2 + 4] = [-4.950, 9, 8.950]

C = [0, 9, 4] + 9/|[0,-2,0]|·[0, -2, 0] + 7/|[-2, 0, 2]|·[-2, 0, 2] = [- 7/2·√2, 0, 7/2·√2 + 4] = [-4.950, 0, 8.950]

D = [0, 9, 4] + 9/|[0,-2,0]|·[0, -2, 0] = [0, 0, 4]

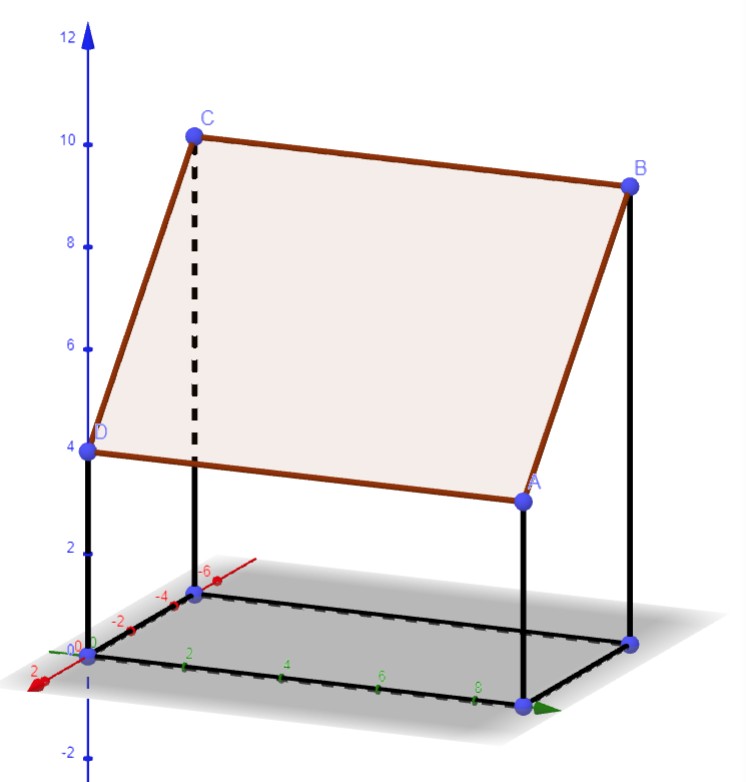
Hier eine Skizze der Dachfläche