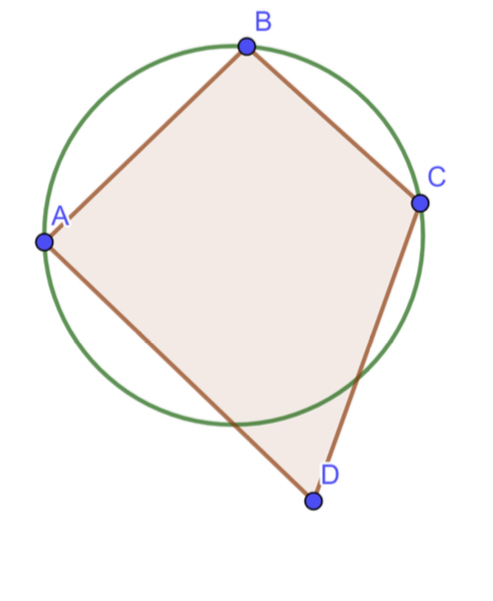
Untersuchen Sie mit Hilfe von GeoGebra, welche Vierecke einen Umkreis besitzen. Dabei konstruieren Sie zuerst ein beliebiges Viereck \( A B C D \). Dann erzeugen Sie einen Kreis durch die Punkte \( A, B \) und \( C \), wobei Punkt \( D \) frei beweglich bleibt und nicht unbedingt auf dem Kreis liegen soll (s. Abb. unten).
Was muss für das Viereck \( A B C D \) erfült sein damit Punkt \( D \) auf dem Kreis liegt?
Lassen Sie verschiedene (für die Untersuchung relevante) Charakteristiken des Vierecks als dynamischen Text anzeigen und beobachten Sie, wie sie sich ändern, wenn Sie den Punkt \( D \) bewegen bzw. wenn der Punkt \( D \) auf dem Kreis liegt.
Basierend auf Ihrer Untersuchung formulieren Sie eine allgemeine Bedingung an ein Viereck, welche die Existenz seines Umkreises sichert. Schreiben Sie diese Bedingung als Text neben der Grafik auf. Überprüfen Sie mit einem wahr-falschBericht, ob für Ihr Viereck \( A B C D \) diese Bedingung erfüllt ist.
Mein Ansatz/Idee:
Erstmal den Mittelpunkt des Kreises (E) bestimmen. Wenn D auf dem Kreis liegt, dann muss der Abstand DE genauso groß sein wie der Abstand AE,BE und CE.
Ich weiß jetzt allerdings nicht, was mit Charakteristiken des Vierecks gemeint ist und wie die dich verändern, wenn Punkt D sich bewegt/auf dem Kreis liegt.
Und den letzten Part der Aufgabe verstehe ich gar nicht.