Zeige dass eine Folge nicht beschränkt ist mithilfe einer Metrik

Question

Aufgabe: Zeige dass eine Folge nicht beschränkt ist mithilfe einer Metrik

Problem/Ansatz:

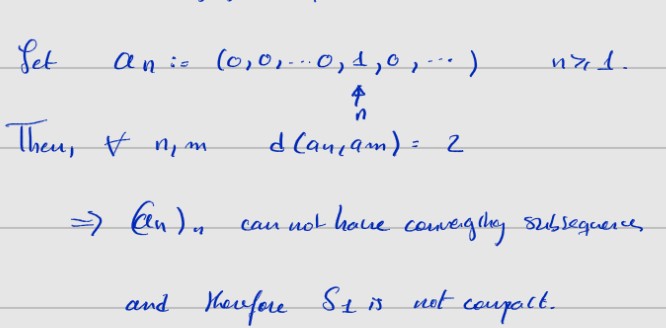
Text erkannt:

Let \( a_{n}:=(0,0, \ldots, 1,0, \ldots) \quad n \geqslant 1 \).
Then, \( \forall n, m \quad d\left(a_{n}, a_{m} m\right)=2 \)
\( \Rightarrow\left(a_{n}\right)_{n} \) can not have convergithy subsequerces and thenfore \( S_{1} \) is not compact.

Im Bild seht ihr die Lösung die ich nicht verstehe. Das Ziel, ist es zu zeigen, dass S1 nicht kompakt ist. Dazu wurde bewiesen, dass die Folge a_n welche in S1 liegt, keine konvergenten Teilfolgen hat und dementsprechend nicht beschränkt sein kann → S1 nicht kompakt

Nun verstehe ich nicht, wie aus d(an, am) = 2 ==> an hat keine konv. Teilfolgen folgt. Warum braucht man a_m um Aufschluss über a_n zu bekommen?

Comments

Der Ausdruck \(d(a_n,a_m)\) sollte Dich an ein sehr berühmtes Kriterium erinnern, dass für Konvergenz notwendig ist - und in vielen Fällen auch hinreichend.

---

Wie ist denn d definiert?

Answer 1

Nun verstehe ich nicht, wie aus d(an, am) = 2 ==> an hat keine konv. Teilfolgen folgt. Warum braucht man a_m um Aufschluss über a_n zu bekommen?

Es folgt, dass \((a_n)_n\) keine konv. TF hat. Nicht \(a_n\). Verwechsle nicht die Folge \((a_n)_n\) mit dem Vektor \(a_n\). Es sind \(a_n\) und \(a_m\) zwei Folgenglieder der Folge \((a_n)_n\), und wenn sie verschieden sind (die Bedingung fehlt), ist deren Abstand 2. Dann überlege (siehe Hinweis oben, "sehr berühmtes Kriterium"....).

Nebenbei: Zur vollständigen Aufgabenstellung gehört die Angabe in welchem Raum wir sind mit welcher Metrik. Und zum Titel: beschränkt ist die Folge durchaus.