Aufgabe:
Veranschaulichen Sie die Lösbarkeit der linearen diophantischen Gleichung ax + by = c. Ihre Lösung soll die folgenden Elemente beinhalten:
(a) Drei Schieberegler für die Koeffizienten a, b und c im Bereich von -25 bis 25.
(b) Ein weitmaschiges Koordinatengitter.
(c) Die Gerade ax + by = c für reelle x und y.
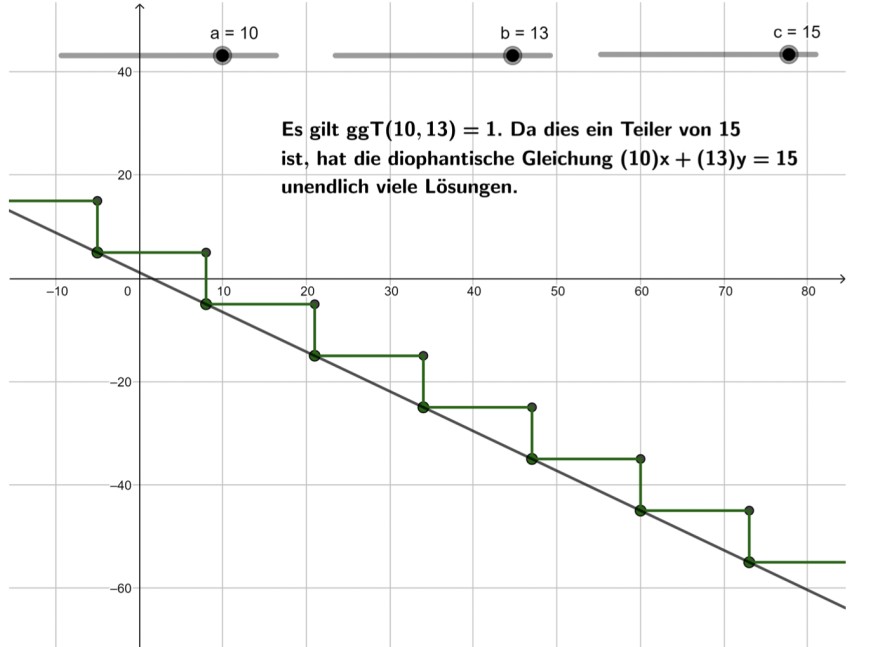
(d) Die ganzzahligen Punkte auf der Geraden (d.h. die Lösungen der diophantischen
Gleichung) im Bereich von -70 bis 70.
Hinweis: Erstellen Sie mit Hilfe von Folgen alle ganzzahligen Punkte (x, y) ∈ Z2 mit −100 ≤ x, y ≤ 100. Wählen Sie davon dann diejenigen aus, die auf der Gerade liegen. Hierfür können die Befehle "Reduzieren" und "BehalteWenn" sinnvoll sein. Informieren Sie sich außerdem, wie Sie die x- bzw y-Koordinate eines Punktes erhalten.
(e) Eine Visualisierung der Tatsache, dass die Lösung der diophantischen Gleichung ax + by = c äquidistante Punkte auf der Geraden sind.
Hinweis: Sie können z.B. eine Art “Steigungsdreieck” (d.h. eine horizontale und eine vertikale Strecke) zwischen je zwei aufeinanderfolgenden Punkte zeichnen. Informieren Sie sich dafür, wie Sie einzelne Elemente einer Folge ansteuern können und wie Sie die Länge einer Folge erhalten.
(f) Ein dynamischer Text, der je nach Wahl der Koeffizienten a,b und c anzeigt, ob die diophantische Gleichung keine oder unendlich viele Lösungen hat.
Hinweis: Erstellen Sie zwei Texte (einen, dass die Gleichung unendlich viele Lösungen hat und einen, dass die Gleichung keine Lösungen hat) und lassen Sie je nach Wahl von a, b, c nur den richtigen anzeigen.
Problem/Ansatz:
Wie veranschauliche ich die ganzzahligen Punkte auf der Geraden (d.h. die Lösungen der diophantischen
Gleichung) im Bereich von -70 bis 70? Teilaufgabe (d).