Aufgabe:
Berechnen Sie den Inhalt der markierten Fläche mithilfe von Stammfunktionen
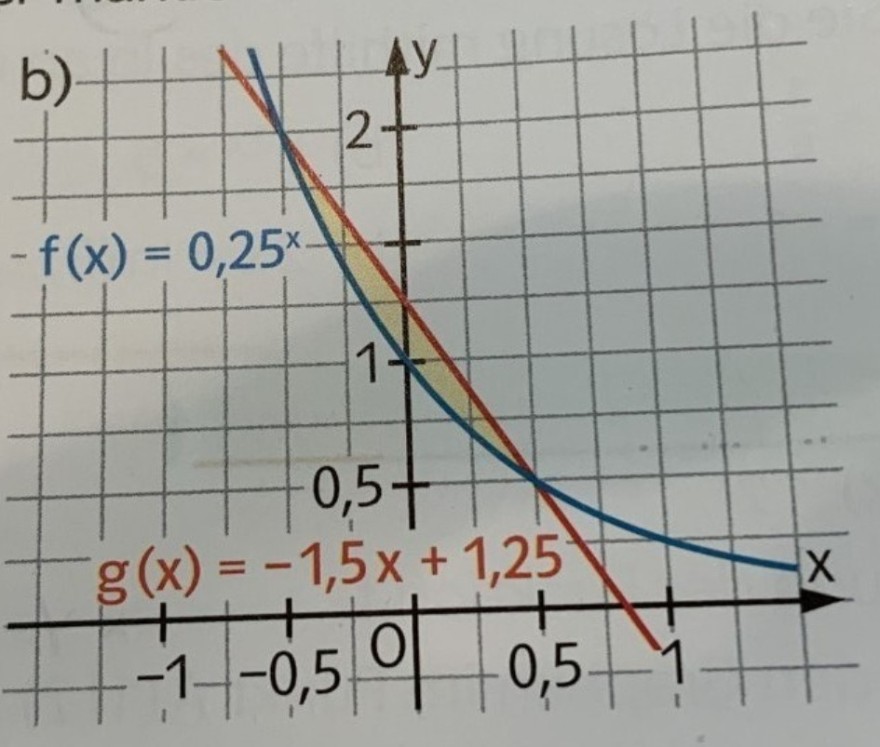
Problem/Ansatz:
Ich bekomme die Stammfunktionen aufgestellt, allerdings, bekomme ich den Flächeninhalt ( Lösung soll wohl 0,168 sein) nicht raus. Wo könnte der Fehler in meiner Berechnung liegen?

Text erkannt:
\( \begin{array}{l}\left(\text { Sb) } f(x)=0,25^{x}\right. \\ f(x)=\frac{1}{\ln (0,25)} \cdot 0,25^{x}=\frac{0,25^{x}}{\ln (0,25)} \\ g(x)=-1,5 x+1,25 \\ G(x)=\frac{-0,75 x^{2}+1,25 x}{-0.0,5(x) \cdot d x} \\ A \int \limits_{-0,5}^{0,5} g(x) \cdot d x-\int \limits_{-0,5}^{0,5}\left(-1,5 x+1,25-\frac{0,25 x}{f}\right) \cdot d x=[ \\ =\left[-0,75 x^{2}+1,25 x-\frac{0,25 x}{\ln (0,25)}\right]_{-0,5}^{0,5}\end{array} \)