Nach langer Zeit mal wieder eine Herausforderung: weitere Lösungen zu finden, als die primitive.
(nichts für Schüler; nur für interessierte, die über den "Tellerrand schauen" wollen)
Wie nudger bereits richtig kommentierte, gibt es unendlich viele Lösungen, weil der Aufgabensteller vergessen hat, Randbedingungen sauber zu definieren. (wir leben nicht mehr im Mittelalter, sondern die theoretische Mathematik ist unendlich vielfältig)
zu "Ansatz":
a) primitive https://de.wikipedia.org/wiki/Polynominterpolation
Auf Seiten wie http://www.gerdlamprecht.de/Mittelwerte.html
braucht man nur die Folge per Komma getrennt eingeben und bekommt unten das Polynom heraus:
y[i]: 7,8,10,13,17,22
ergibt bei Voreinstellung x[i]: 0,1,2,..
f(x)=7+x*1/2+pow(x,2)*1/2+pow(x,3)*0+pow(x,4)*0+pow(x,5)*0 mit pow(x,2)=x² ;pow(x,3)=x^3 usw.
Da viele jedoch bei Index 1 statt 0 beginnen und ich auch gern die Vorgänger noch wissen möchte, x[i]: 1,2,..
ergibt 7-x*1/2+pow(x,2)*1/2 =(x^2 - x)/2 + 7
b) wenn die Folge nicht mit 7,7,... beginnen soll, gibt man einfach davor eine 6 ein und bekommt bei 7 Schnittstellen ein Polynom 6. Grades: f(n)= 6 - n*(-1404 + n*(1264 + n*(-735 + n*(175 + (n - 21)*n))))/720
c) die von döschwo angegebene Folge https://oeis.org/A005709 ist jedoch wegen der vorderen Stellen:
1, 1, 1, 1, 1, 1, 2, 3, 4, 5, 6, 7, 8,... etwas anders, weil sie aus der rekursiven Welt kommt: a(n) = a(n-1) + a(n-7)
Diese in die gesuchte explizite Funktion zu wandeln ist für Schüler unmöglich. Die moderne Mathematik kennt jedoch hypergeometrische Funktionen:
f(n)=HypergeometricPFQ[{-(11/7)-n/7,-(10/7)-n/7,-(9/7)-n/7,-(8/7)-n/7,-1-n/7,-(6/7)-n/7,-(5/7)-n/7},{-(11/6)-n/6,-(5/3)-n/6,-(3/2)-n/6,-(4/3)-n/6,-(7/6)-n/6,-1-n/6},-(823543/46656)]
Alle 3 kann man auch (weich) plotten, um die Gleichheit an den geforderten 6 Stützstellen zu sehen (explizite Formeln erlauben ja stufenlose Übergänge statt nur ganzzahlige Argumente):
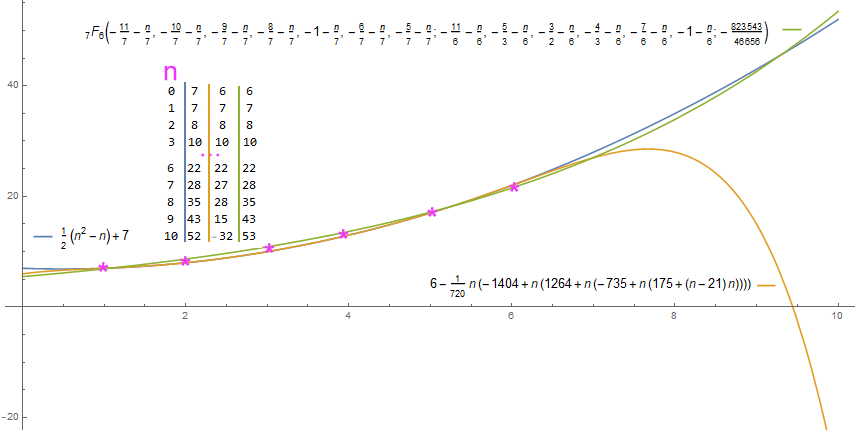
d) trigonometrische Interpolation... keine Zeit mehr...
Grüße