Parallele Geradengleichung ausrechen mit P1, P2 und P3

Question

Aufgabe:

Eine Gerade g geht durch die Punkte P₁ und P₂. Die Gerade h ist parallel zu g und geht durch den Punkt P₃. Notiere die Geradengleichungen für g und h.

A1)

P1 : (2;5)

P2: (4;4)

P3: (0;0)

A2)

P1 = (-1;2)

P2 = (1;8)

P3 = (2;3)
Problem/Ansatz:

Ich war leider in der Mathe stunde nicht da und konnte aus dem Grund die Aufgabe nicht bearbeiten im Internet hab ich nach einem Video gesucht aber nichts gefunden es wäre total nett wenn jemand mir die Aufgabe lösen würde mit rechenweg so lerne ich es am beste danke. :)

Comments

Kannst du ausrechnen, welchen Anstieg eine Gerade hat, die durch die Punkte P1 : (2;5) und
P2: (4;4) verläuft?

(Das müsste vor der einen Stunde behandelt worden sein, die du versäumt hast.)

Wenn du das beantwortet hast, lösen wir gemeinsam den Rest der Aufgabe.

---

Da habe ich ja gerade noch rechtzeitig gesehen, lieber Rechenschieber, dass du wieder pädagogisch unterwegs bist, bevor ich meine Antwort rausgehauen habe.

Aber ich gebe Tom ein kleine Hilfestellung in Sachen Steigung.

Du bestimmst die Steigung \( m \) zwischen 2 Punkten mit der Formel \( \displaystyle m=\frac{y_{1}-y_{2}}{x_{1}-x_{2}} \) 

---

Es hat sie auf mathe online . de schon jemand gefunden, der die Lösung rausgehauen hat.

---

Dann stelle ich meine Antwort doch gleich ein, damit die Frage nicht unbeantwortet bleibt.

---

Parallele gerdangleichung ausrechen

An wen soll Gerd sich denn angleichen?

☺

---

An Gazprom?                .

Answer 1

oder so:

A1:

y= g(x) =mx+b

g(1) = 5

g(4) = 4

m+b= 5

4m+b = 4

subtrahieren:

-3m= 1

m= -1/3

-> -1/3+b = 5

b= 5 1/3 = 16/3

h hat dieselbe Steigung wie g:

h(x) = -1/3*x+b

h(0)= 0

0+b = 0

h(x) = -1/3*x (Ursprungsgerade, erkennbar an P3)

A2 geht analog.

Answer 2

Hallo Tom,

die allgemeine Form einer Geradengleichung kannst du schreiben als y = mx + n.

m ist dabei die Steigung und n der Schnittpunkt der Geraden mit der y-Achse.

Du bestimmst die Steigung \( m \) zwischen 2 Punkten mit der Formel \( \displaystyle m=\frac{y_{1}-y_{2}}{x_{1}-x_{2}} \)

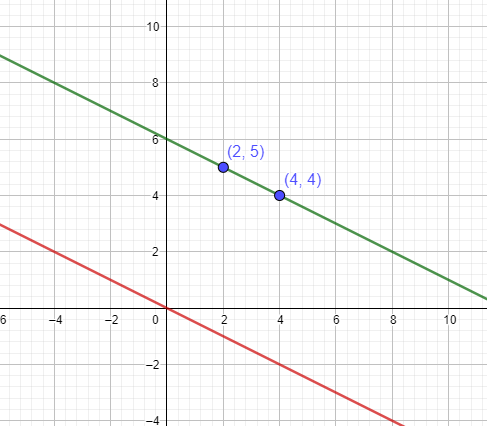
Du hast Punkte \( P_1=\left(x_{1} \mid y_{1}\right)=(2 \mid 5) \quad \) und \( \quad P_2=\left(x_{2} \mid y_{2}\right)=(4 \mid 4) \), wobei die Koordinaten für \( \mathrm{x} \) und \( \mathrm{y} \) auch vertauscht werden können.

Setze die Koordinaten in die Formel ein.

\(m=\frac{5-4}{2 - 4}=-\frac{1}{2}\) oder -0,5, falls du lieber mit Dezimalzahlen rechnest.

Um n zu bestimmen, setzt du dein Ergebnis für m und die Koordinaten eines Punktes in die Geradengleichung ein.

Somit lautet die Gleichung für g y = -0,5x + 6.

Wenn zwei Geraden parallel sind, haben sie die gleiche Steigung. Also brauchst du nur noch die Koordinaten von P3 in die Gleichung einsetzen. Das ist bei der 1. Aufgabe aber nicht nötig, weil h durch den Ursprung (= Schnittpunkt mit y-Achse) verläuft. Die entsprechende Gleichung lautet also y = -0,5x

Die 2. Aufgabe kannst du genau so rechnen.

Gruß, Silvia

Answer 3

Eine Gerade g geht durch die Punkte P1 und P2. Die Gerade h ist parallel zu g und geht durch den punkt P3. Notiere die Geradengleichungen für g und h.

P1(2 | 5) ; P2(4 | 4) ; P3(0 | 0)

Gerade durch P1 und P2

Steigung m

m = (y2 - y1)/(x2 - x1) = (4 - 5) / (4 - 2) = - 1/2

Lineare Funktion g mit Punkt P1 und der Steigung m in der Punkt-Steigungsform aufstellen und ausmultiplizieren.

g(x) = - 1/2·(x - 2) + 5 = - 1/2·x + 6

Lineare Funktion h mit dem Punkt P3 und der Steigung m aufstellen

h(x) = - 1/2·(x - 0) + 0 = - 1/2·x

Skizze

~plot~ {2|5};{4|4};{0|0};-1/2x+6;-1/2x;[[-8|8|-6|6]] ~plot~