Wäre somit jetzt gezeigt, dass d* eine Metrik ist ohne alle 3 Metrik-Axiome zu beweisen?

Question

Aufgabe:

wollte zeigen dass

d* : ℝ² x ℝ² ---> ℝ

d*(x,y) = 2 | x1 - y1 | + 3 | x2 - y2 |   äquivalent zur Maximumsnorm ist.

Problem/Ansatz: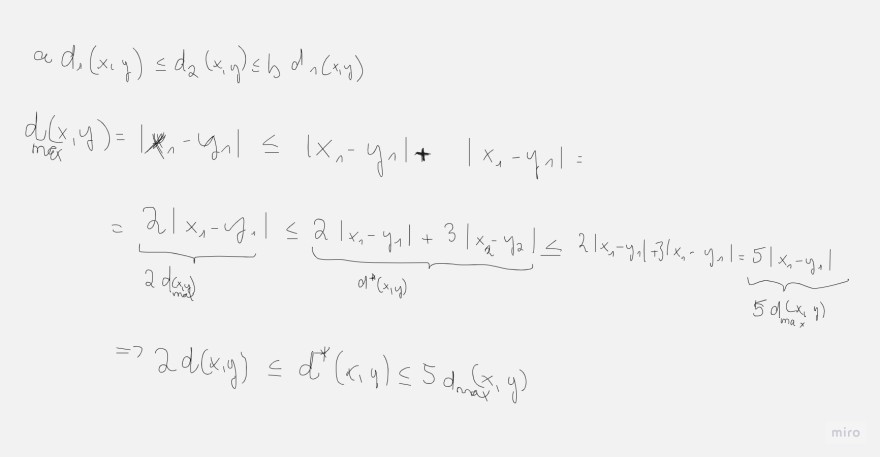

Text erkannt:

\( \begin{array}{l} \Rightarrow 2 d(x, y) \leq d^{*}(x, y) \leq 5 d_{\text {max }}(x, y) \\ \end{array} \)
miro

Wäre somit jetzt gezeigt, dass d* eine Metrik ist ohne alle 3 Metrik-Axiome zu beweisen?

LG

Comments

Wie kommst du zu der Aussage , dass die Maximumnorm  |x1-y1| ist?  ist das überhaupt irgendeine Norm?

(übrigens später wieso ist |x2-y2|<=|x1-y1| aber das spielt keine Rolle mehr)

lul

---

@ lul: Ich nehme an, B wollte sagen sei \(d_{\infty}(x,y)=|x_1-y_1|\) (oBdA)....

---

Hallo

aber |x1-y1| ist doch gar keine Metrik? denn |x2-y2|können beliebig groß werden, bei |x1-y1| beliebig klein?

lul

---

@ lul: Ich nehme an, B wollte sagen sei \(d_{\infty}(x,y)=|x_1-y_1|\) (oBdA)....

Dies nur als Erklärungsversuch für den Text von Bosna. Richtig / Vollständig erklärt ist das nicht, auch wenn die letztendliche Abschätzung stimmt.

Answer 1

Die Antwort auf die Frage, ob aus den Ungleichungen folgt, dass \(d^{\ast}\) die 3 Metrik-Axiome erfüllt, ist: Nein.