Manchmal braucht eine mathematische Problemlösung einen ‚Geistesblitz‘. Ob sich dieser Geistesblitz einstellt oder nicht ist offenbar reine Glückssache. Es gibt kaum kognitive Handlungen, welche die Chance auf einen Geistesblitz erhöhen. Ein Mathematiktreibender kann seine Chancen in diesem Zusammenhang etwas erhöhen, wenn er Strategien des Repräsentationswechsels beherrscht.
Es gibt kein Denken ohne Zeichen. Mathematische Probleme müssen in Zeichenform vorliegen, um sie überhaupt einer Lösung näherzubringen. Die Darstellung mathematischer Probleme kann innerhalb der Regeln eines konsistenten Darstellungssystems äußerlich verändert werden, ohne ihre Inhalte zu verlieren. Eine solche Veränderung nennt man ‚Repräsentationswechsel‘. In der Schulmathematik finden Repräsentationswechsel insbesondere bei Term- oder Gleichungsumformung oder im Wechsel zwischen Punktmengen in einer Wertetabelle und Punktmengen in einem Koordinatensystem statt.
Der Perspektivwechsel ist eine Sonderform des Repräsentationswechsels, wenn die Repräsentation eines Sachverhaltes äußerlich unverändert vor dem geistigen Auge verändert wird. Als Beispiel für einen Perspektivwechsel sei der Beweis des Satzes von Desargues angeführt.
Satz von Desargues:
Auf dem Strahl PA liegt A‘. Auf dem Strahl PB liegt B‘. Auf dem Strahl PC liegt C‘. AC schneidet A’C‘ in R. AB schneidet A’B‘ in S BC schneidet B’C‘ in T (siehe Abbildung; alle Schnittpunkte sollen im Endlichen liegen).
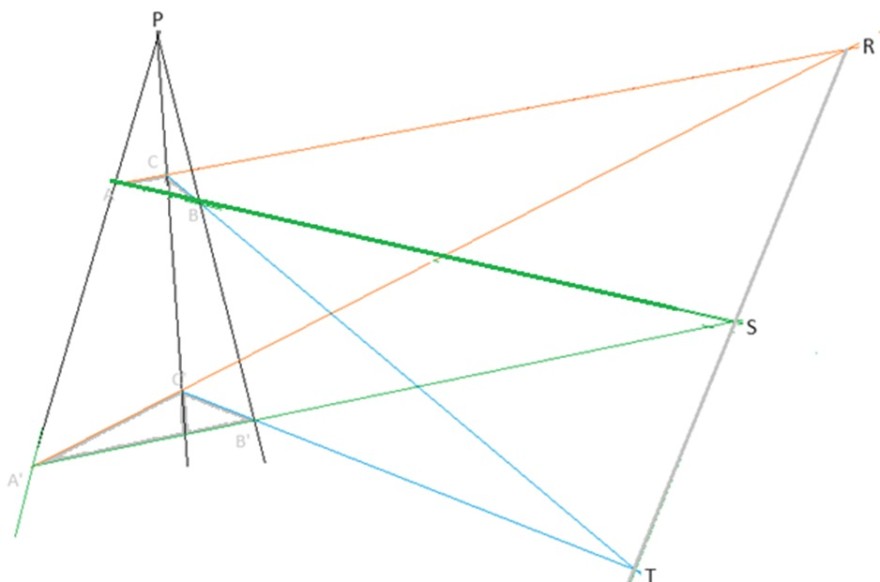
Dann liegen R, S und T auf einer Geraden.
Eine Beweisidee zu diesem Satzes wird nahegelegt, wenn man der vermeintlich ebenen Anordnung von Punkten eine räumliche Anordnung unterlegt, also die Perspektive des geistigen Auges auf die gegebene Darstellung verändert. Um den Betrachter bei dieser Veränderung der Perspektive zu unterstützen, werden die Dreiecke ABC und A’B’C‘ grau unterlegt und dazu aufgefordert, sie als definierende Dreiecke zweier Ebenen EABC und EA’B’C‘ zu sehen.
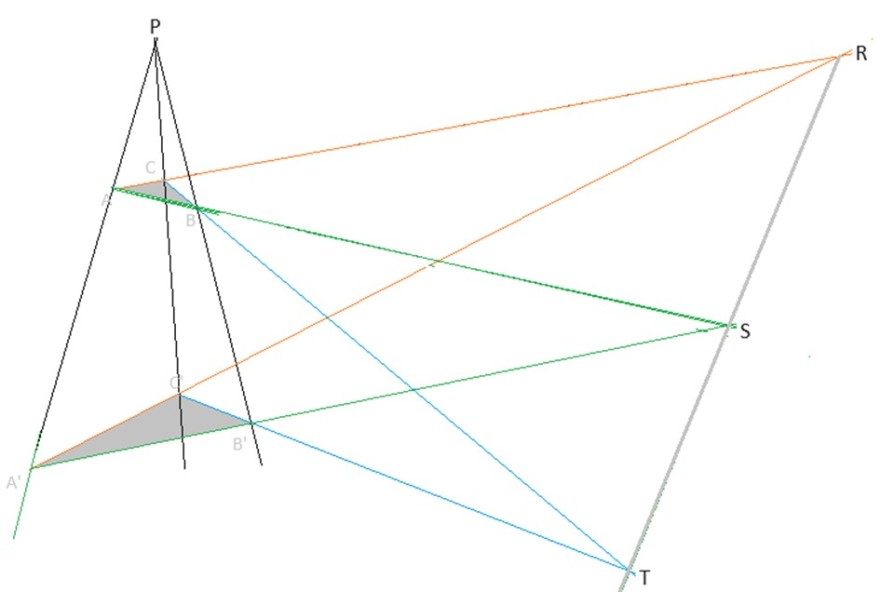
Dann wird erkennbar, dass sich die Ebenen EABC und EA’B’C‘ in einer Geraden g schneiden. Es bleibt zu zeigen, dass R, S und T auf dieser Geraden g liegen müssen. Dies wird exemplarisch deutlich, wenn man die Ebene EPAB mit den Ebenen EABC und EA’B’C‘ schneidet. Es entstehen die grünen Schnittgeraden, die sich in S schneiden und S muss, da S sowohl auf EABC als auch auf EA’B’C‘ liegt, auf g liegen.