Hypothesentest; Signifikanzniveau; Entscheidungsregel

Question

Aufgabe:

1. In einer Schule mögen angeblich 40% der Schülerinnen und Schüler (SuS) das Fach Mathematik. Die Kurslehrer der Stufe sind davon überzeugt, dass es mehr SuS gibt, die Mathe mögen, und will, dass Sie das mit Hilfe eines Hypothesentests überprüfen.
Es werden alle 90 SuS der Jahrgangsstufe befragt, der Einfachheit halber sollen nur „Ja-Nein"-Antworten möglich sein.
a) Führen Sie einen geeigneten Hypothesentest durch und geben Sie unter der Voraussetzung, dass das Signifikanzniveau 5% beträgt, eine Entscheidungsregel an.
b) Erläutern Sie was ein Fehler 1. Art (a - Fehler ) ist und geben Sie seine
Größe im aktuellen Hypothesentest an

Comments

es werden alle 90 SuS der Jahrgangsstufe befragt

Ich halte es für problematisch, das Ergebnis der Befragung einer einzigen Jahrgangsstufe auf die gesamte Schule zu verallgemeinern.

---

Answer 1

Du brauchst einen rechtsseitigen Hypothesentest gemäß folgender Wahrscheinlichkeitsverteilung.

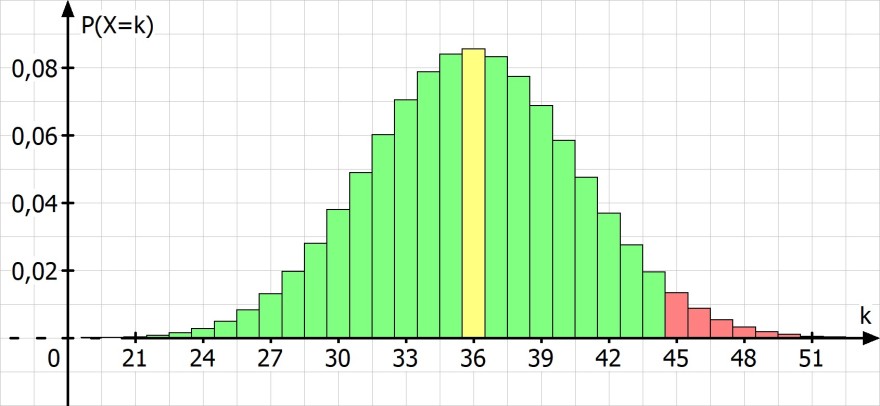
a)

Die Nullhypothese kann bei höchstens 44 von 90 Schüler die mit ja antworten nicht abgelehnt werden.

Die Nullhypothese wird ab 45 ja antworten abgelehnt. In dem Fall würde man glauben das der Anteil die Mathe mögen über 40% liegt.

b)

Der Alpha-Fehler ist die Wahrscheinlichkeit das die Nullhypothese ablehnt, obwohl sie zutreffend ist. Oder im Sachkontext, dass man glaubt das Mehr als 40% der Schule Mathe mögen obwohl dies nicht zutreffend ist.

Comments

Kann man dies auch anders als mit diesem Schaubild ausrechnen? Also wie mit einem TR

---

Rechenwege richten sich danach wie ihr es gemacht habt. Einige dürfen den Taschenrechner zur Beantwortung Nutzen andere müssen die Normalverteilung mit den Sigmaregeln als Näherung nutzen.

Die kritische Grenze von 44 würde ich wie folgt berechnen:

NORMAL(k) = 0.95 --> k = 1.645

K = n·p + k·√(n·p·q) = 90·0.4 + 1.645·√(90·0.4·0.6) = 43.65 ≈ 44

---

Wurden denn dann hier das, dass Signifikanzniveau 5% beträgt berücksichtigt?

---

Wurden denn dann hier das, dass Signifikanzniveau 5% beträgt berücksichtigt?

Natürlich. Das Signifikanzniveau ist doch das entscheidendste bei einem Signifikanztest.

Dabei sind das in den überwiegenden Fällen aber meist 5% weshalb man die Sigma-Intervalle dafür kennen sollte.