Hallo ihr Lieben,
ich habe ein Problem bei folgender Aufgabe. Ich soll eine Taylorentwicklung machen und schlussendlich als Summenformel angeben. Die Taylorentwicklung habe ich hinbekommen, mein Problem ist das finden der K-Ableitung (das Muster erkennen). Bei anderen Taylorentwicklungen habe ich das hinbekommen, bei dieser leider nicht. Könntet ihr mir erklären, wie man das angeht, ohne das man das einfach stumpf ausprobiert.
Einen Teil der K-Ableitung habe ich bereits gefunden, aber der Zähler ist mir unbekannt.
Die Aufgabenstellung lautet:
Text erkannt:
2 Taylorentwicklung (6 Punkte)
Berechnen Sie für die Funktion
\( f(x)=\frac{1}{\sqrt{1+2 x}} \)
so viele Terme der Taylorentwicklung um \( x_{*}=0 \) bis Sie das Muster erkennen, und geben Sie dann die gesamte Taylorreihe als Summenformel an.
Ansatz:
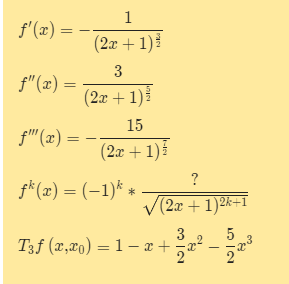
Text erkannt:
\( \begin{array}{l}f^{\prime}(x)=-\frac{1}{(2 x+1)^{\frac{3}{2}}} \\ f^{\prime \prime}(x)=\frac{3}{(2 x+1)^{\frac{5}{2}}} \\ f^{\prime \prime \prime}(x)=-\frac{15}{(2 x+1)^{\frac{7}{2}}} \\ f^{k}(x)=(-1)^{k} * \frac{?}{\sqrt{(2 x+1)^{2 k+1}}} \\ T_{3} f\left(x, x_{0}\right)=1-x+\frac{3}{2} x^{2}-\frac{5}{2} x^{3}\end{array} \)