Wahrscheinlichkeit ausrechnen armbanduhren

Question

Problem/Ansatz:

Ich verstehe es nicht.

Text erkannt:

1.57 Armbanduhren
sRDP
$A B$ Ein Unternehmen produziert Armbanduhren.
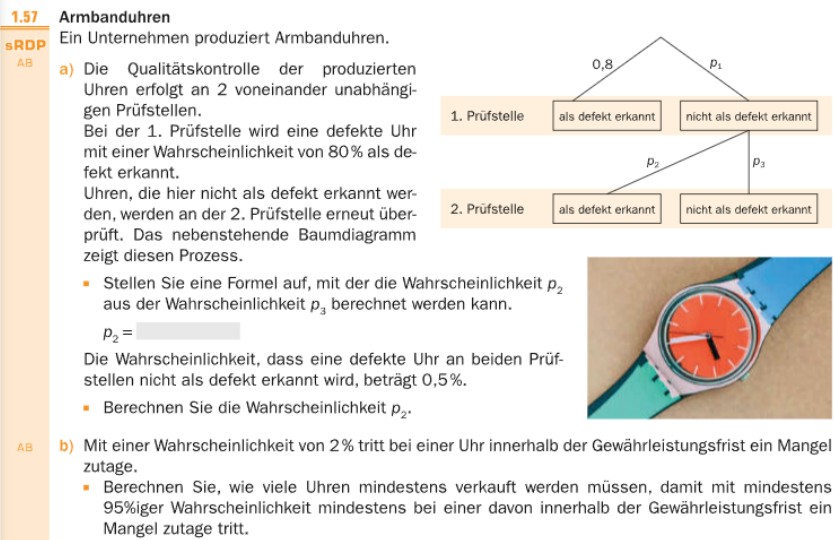
a) Die Qualitätskontrolle der produzierten Uhren erfolgt an 2 voneinander unabhängigen Prüfstellen.
Bei der 1. Prüfstelle wird eine defekte Uhr mit einer Wahrscheinlichkeit von $80 \%$ als defekt erkannt.
Uhren, die hier nicht als defekt erkannt werden, werden an der 2. Prüfstelle erneut überprüft. Das nebenstehende Baumdiagramm zeigt diesen Prozess.
- Stellen Sie eine Formel auf, mit der die Wahrscheinlichkeit $p_{2}$ aus der Wahrscheinlichkeit $p_{3}$ berechnet werden kann.
$p_{2}=$
Die Wahrscheinlichkeit, dass eine defekte Uhr an beiden Prüfstellen nicht als defekt erkannt wird, beträgt 0,5\%.
- Berechnen Sie die Wahrscheinlichkeit $p_{2}$.
1. Prüfstelle
2. Prüfstelle
b) Mit einer Wahrscheinlichkeit von $2 \%$ tritt bei einer Uhr innerhalb der Gewährleistungsfrist ein Mangel zutage.
" Berechnen Sie, wie viele Uhren mindestens verkauft werden müssen, damit mit mindestens 95\%iger Wahrscheinlichkeit mindestens bei einer davon innerhalb der Gewährleistungsfrist ein Mangel zutage tritt.

Answer 1

a)

p2 = 1 - p3

0.2 * p3 = 0.005 --> p3 = 0.025
p2 = 1 - 0.025 = 0.975

b)

1 - (1 - 0.02)ⁿ = 0.95 --> n = 148.3

Es müssen mind. 149 Uhren verkauft werden.