Wahrscheinlichkeit ausrechnen bei Anwendungsaufgaben?

Question

Aufgabe:

Herbert und Georg haben je zwei Steine. Sie werfen abwechseln auf eine Blechdose. Ihre Treffsicherheiten betragen \( \frac{1}{3} \) beziehungsweise \( \frac{1}{4} \)

a) Wie groß ist die Wahrscheinlichkeit, dass Herbert als erster trifft wenn er beginnt?

b) Wie groß ist die Wahrscheinlichkeit, dass Georg als erster trifft, wenn er beginnt?

Problem/Ansatz:

ich verstehe nicht wie man darauf kommt. Unser Lehrer hat uns die Lösungen zum Kontrollieren mitgegeben und da ist der Rechenansatz für a) so: \( \frac{1}{3} \) + \( \frac{2}{3} \) · \( \frac{3}{4} \) · \( \frac{1}{3} \) = \( \frac{1}{3} \) + \( \frac{1}{6} \) = 0,5

für b)

\( \frac{1}{4} \) + \( \frac{3}{4} \) · \( \frac{2}{3} \) · \( \frac{1}{4} \) = \( \frac{1}{4} \) +\( \frac{1}{8} \) =\( \frac{3}{8} \)

Ich verstehe nicht wie man darauf kommen soll.

Comments

Wer hat denn welche Treffsicherheit?

---

Herbert hat eine Treffsicherheit von 1/3

und Georg von 1/4

Answer 1

a) so: 1/3 + 2/3 · 3/4 · 1/3 = 1/3 + 1/6 = 0,5

Besser verständlich mit einem Baum:

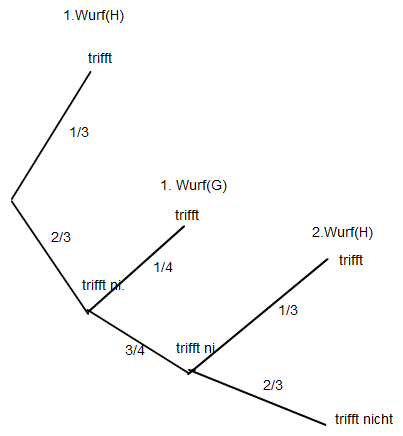
Es gibt nur zwei Äste zu dem Ereignis

"Herbert trifft als erster"

Wenn Herbert als 1. wirft, kann es sein, dass er gleich beim ersten Wurf trifft

(Wahrscheinlichkeit 1/3) . Mit der Wahrscheinlichkeit 2/3 trifft er nicht (2. Ast)

Dann ist G dran. Wenn er trifft, kann das gesuchte Ereignis nicht

mehr eintreten, ansonsten  (Der Ast mit den 3/4 ) tritt es noch ein, wenn er beim

2. Wurf trifft. also der Ast mit  2/3 · 3/4 · 1/3.

Die Summe der beiden Pfadwahrscheinlichkeiten ist also das

gesuchte Ergebnis.

Mit so einem ähnlichen Baum schaffst du auch b).

Comments

warum muss ich dann aber nicht alles multiplizieren sondern nur einen Teil davon?

---

Du musst längs des Pfades multiplizieren und

die Ergebnisse der beiden Pfade addieren.

Answer 2

Herbert 1/3
Georg 1/4

a.)
Herbert beginnt
Mit dem 1. Wurf 1/3 = 33.33 %

mit dem 2. Wurf nur dann wenn Georg nicht trifft
2/3 * ( Herbert nicht getroffen )
3/4 * ( georg nicht getroffen )
1/3 ( Herbert getroffen ) = 16.66 %

zusammen : 50 %

b.) Georg beginnt
1/4 + 3/4 * 2/3 * 1/4
0.25 + 0.125 = 37.5 %