Doppelintegral - Integrationsreihenfolge vertauschen

Question

Hallo Leute,

hier die eigentliche Aufgabe. Mein Problem ist unten drunter geschildert. Danke im voraus! :)

Text erkannt:

10 Doppelintegral (5 Punkte)
Es soll ein Flächenintegral
$\int \limits_{M} \phi(\vec{r}) \mathrm{d} a$
über das nebenstehend dargestellte Gebiet $M$ der $x$ - $y$-Ebene berechnet werden. Die Ränder sind Kreisabschnitte deren Radien und Mittelpunkte Sie der Darstellung entnehmen.
Schreiben Sie das Flächenintegral als Doppelintegral mit expliziten Grenzen. Entscheiden Sie die Integrationsreihenfolge selbst und zerteilen Sie ggf. das Integrationsgebiet, wenn Sie es wünschen.

Problem:

Meine Problem ist leider, dass ich nicht wirkliche verstehe, wann genau ich das Integrationsgebiet zerteilen muss. Ich würde gerne bei dieser Aufgabe beide Integrationsreihenfolgen hinbekommen. Ich habe gedacht, dass wenn ich das Integrationsgebiet vertikal parametrisiere und keine Unterbrechungen in den Schnitten auftauchen, ich das Gebiet nicht zerteilen muss (siehe Bild 2). Anscheinend muss ich dies doch noch tun, aber warum? Ich vermute, dass dies nicht geht, da im ersten und zweiten Quadranten jeweils zwei verschiedene Halbkreise auftauchen und somit der y-Wert nicht durch eine Funktion beschrieben werden kann und ich somit gezwungen bin das Integrationsgebiet zu zerteilen. Ist diese Annahme korrekt?

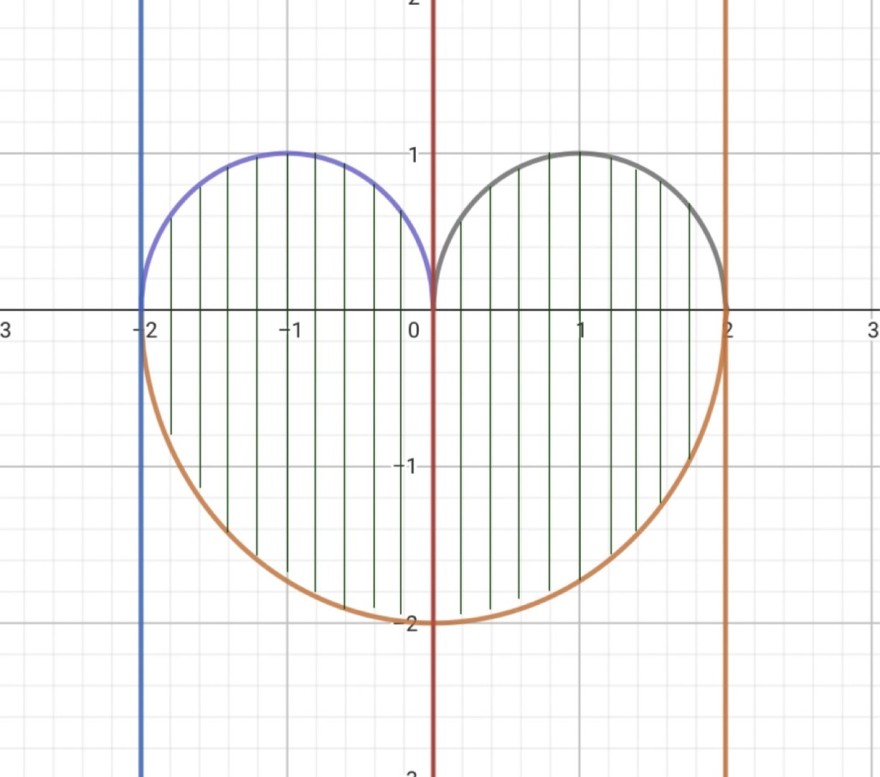
vertikale Parametrisierung (über y, festes x): $$\int \limits_{x=-2}^{x=0}\int \limits_{y=-\sqrt{4-x^2}}^{y=\sqrt{1-(x-1)^2}}Φ (x;y)dydx+ \int \limits_{x=0}^{x=2}\int \limits_{y=-\sqrt{4-x^2}}^{y=\sqrt{1-(x+1)^2}}Φ (x;y)dydx$$

horizontale Parametrisierung (über x, festes y)

Jetzt wollte ich das Gebiet horizontal parametrisieren. Nun sind die Schnitte auf alle Fälle unterbrochen (siehe Bild 3). Nach meiner Logik müsste ich jetzt das Integrationsgebiet zerteilen. Das Problem ist, dass ich nicht genau weiß, wie ich das für diesen Fall machen soll. Meine Idee für den 2ten Fall wäre, dass Gebiet zu zerteilen: Das erste Integral wäre y-Grenzen von [-2; 1] und x-Grenzen von [Umkehrfunktion eines Viertelkreises im III. Quadranten; Umkehrfunktion eines Halbkreises mit Mittelpunkt (-1;0)], das zweite Integral wäre y-Grenzen von [-2; 1] und x-Grenzen von [Umkehrfunktion eines Viertelkreises im IV. Quadranten; Umkehrfunktion eines Halbkreises mit Mittelpunkt (1;0)].

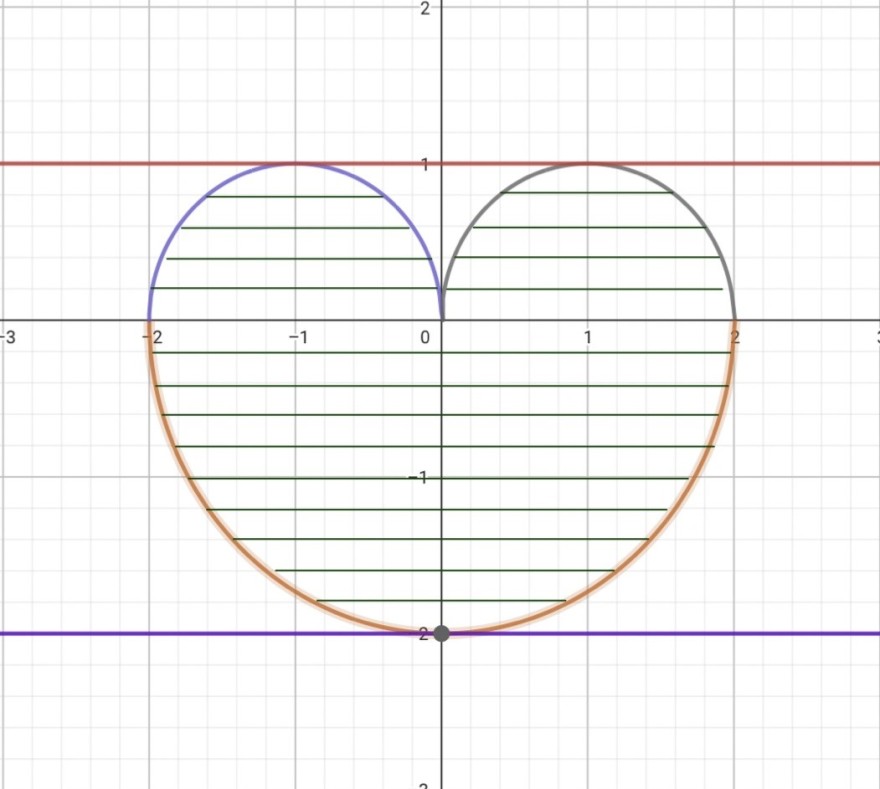
Nun ist mir noch aufgefallen, dass ich gar nicht weiß, wie man aus dem Halbkreis ein Viertelkreis macht und wie ich die Umkehrfunktion bilden kann von den kleinen Halbkreisen.

Ich hoffe, ihr versteht, was ich meine... Bin über jede Hilfe dankbar.

Wäre auch jedem dankbar, der mir das Zerteilen noch einmal genauer erklären kann. Wann ist es wirklich notwendig?

Comments

Hallo

zumindest für die Kreise um 0 ist es doch besser mit Polarkoordinaten zu rechnen?  also über r und φ zu integrieren?

lul

---

Was soll mit der Funktion  φ  gemeint sein ?

Answer 1

In Deinem ersten Fall kannst Du das Integral durchaus ohne Unterteilung notieren. Denn das Gebiet ist beschrieben durch:

$$-2 \leq x \leq 2, \quad -\sqrt{4-x^2} \leq y \leq f(x)\qquad \text{mit}\\\quad f(x):=\sqrt{1-(x+1)^2} \text{ für } x \in [-2,0], \\\quad f(x):=\sqrt{1-(x-1)^2} \text{ für } x \in [0,2],$$

Aber diese Beschreibung ist für das praktische Rechnen unbrauchbar. Aus praktischen Gründen ist also die Unterteilung in 2 Teile hier höchst angebracht. Du hast allerdings die beiden Teile vertauscht.

Anders ist es im anderen Fall, hier hat man 3 Teilgebiete:

$$y \in [0,1], -1-\sqrt{1-y^2} \leq x \leq-1+\sqrt{1-y^2}$$

$$y \in [0,1], 1-\sqrt{1-y^2} \leq x \leq 1+\sqrt{1-y^2}$$

$$y \in [-2,0], -\sqrt{4-y^2} \leq x \leq \sqrt{4-y^2}$$

Comments

Okay, danke für die Hilfe. Also, wenn ich das jetzt richtig verstehe, dann ist die richtige Variante für dydx folgende:

und das eine mögliche für die Variante für dxdy:

Ist das jetzt soweit korrekt? Bitte um Bestätigung. :)

---

Ja, das ist richtig

Answer 2

Oberer linker Halbkreis:

(1)        $(x+1)^2 + y^2 = 1\qquad x\in\mathbb{R},\ y\in [0,1]$

Oberer rechter Halbkreis:

(2)        $(x-1)^2 + y^2 = 1\qquad x\in\mathbb{R},\ y\in [0,1]$

Unterer Halbkreis:

(3)        $x^2 + y^2 = 4\qquad x\in\mathbb{R},\ y\in [-2,0]$

wenn ich das Integrationsgebiet vertikal parametrisiere

Dann wird die linke Hälfte durch (1) und (3) begrenzt und die rechte durch (2) und (3). Also musst du aufteilen.

Jetzt wollte ich das Gebiet horizontal parametrisieren.

Dann wird der Teil oberhalb der $y$-Achse durch (1) und (2) begrenzt und der Teil unterhalb der $y$-Achse durch (3). Also musst du aufteilen.

Comments

Danke für deine Hilfe, vertikal hab ich richtig hinbekommen.

aber laut meinem Prof soll (2) umgestellt nach y=\sqrt{1-(|x|-1)²} noch Betragstriche enthalten. Wenn ich die Betragstriche nicht mache, kommt laut Wolfram Alpha (bekomme das Integral nicht selbstständig gelöst) was komplexes raus, wenn ich für Φ (x,y)=1 einsetze. Das versteh ich nicht.

Horizontal habe ich immer noch Problem das zu verstehen, ist das jetzt so richtig?

Text erkannt:

$\int \limits_{y=0}^{y=1} \int \limits_{x=\sqrt{1-y^{2}}-1}^{x=\sqrt{1-y^{2}}+1} \Phi(x ; y) d x d y+\int \limits_{y=-2}^{y=0} \int \limits_{x=-\sqrt{4-y^{2}}}^{x=\sqrt{4-y^{2}}} \Phi(x ; y) d x d y$