Aufgabe:
Von einer Zahl ist folgendes bekannt: Die Zahl lässt bei Division durch 8 den Rest 2, das Dreifache der Zahl lässt bei Division durch 15 den Rest 9 und das Fünffache der Zahl lässt bei Division durch
11 den Rest 4.
(a) Stellen Sie die Situation durch ein Kongruenzsystem dar.
(b) Bestimmen Sie alle Zahlen z ∈ [0,439), die die obigen Bedingungen erfüllen.
(c) Wie viele solche Zahlen gibt es im Bereich [0, 2000)?
Problem/Ansatz:
a) habe ich hinbekommen, bei b) bin ich mir unsicher. Bei der II Gleichung 3x≡9 Mod 15 rechne ich :3, muss ich dann nur 3:3 und 9:3 rechnen oder auch, wie ich es gemacht habe, die 15:3?
Und c) weiß ich leider gar keinen Ansatz
Text erkannt:
\( 18: 58 \) Montag 2. Okt.
(1)
\( \mathrm{X}=\operatorname{STE}(35) \)
Saslübungen
\( \times \)
Spicker
\( \mathrm{X}=\mathrm{STE}(35) \)
Q.
\( \times \)
Ubung
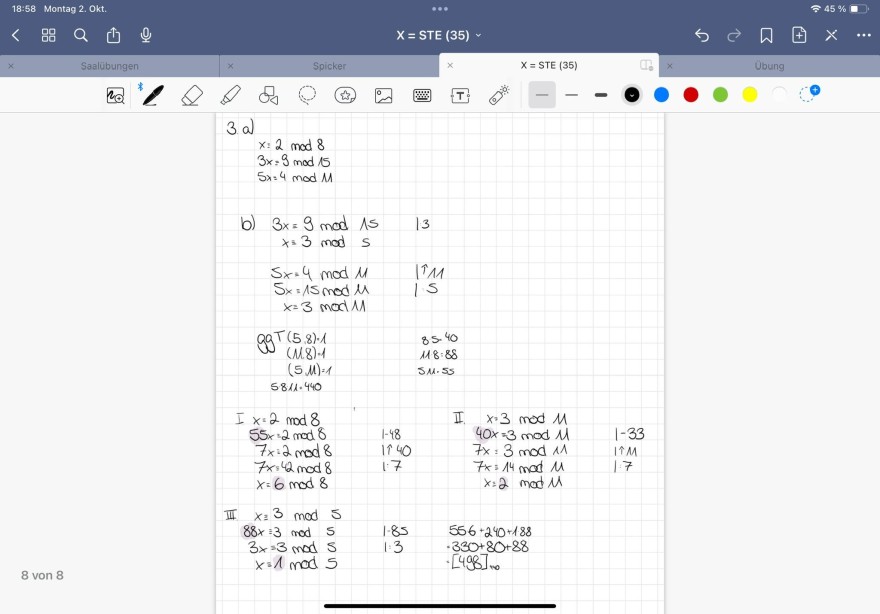
\( 3 a \mathrm{al} \)
\( \begin{array}{l} x=2 \bmod 8 \\ 3 x=9 \bmod 15 \\ 5 x=4 \bmod M \end{array} \)
b)
\( \begin{array}{l} 3 x=9 \bmod 15 \quad 13 \\ x=3 \mathrm{mod} s \\ S x=4 \bmod M \\ 5 x=15 \bmod \mu \\ 1 \uparrow / 1 \\ x=3 \bmod 11 \\ 99 T(5.8) \cdot 1 \\ 85.40 \\ (5 \mu)=1 \\ \text { 118:88 } \\ 5841.440 \\ \text { SM.SS } \\ \end{array} \)
\( \begin{array}{cc} g T^{T}(5.8) \cdot 1 & 85.40 \\ (M .8) \cdot 1 & 118.88 \\ (5 \mu)=1 & 5 M .55 \end{array} \)
8 von 8