zuerst habe ich m ausgerechnet indem ich y2-y1 / x2-x1 gerechnet habe und bin da auf 0,5 gekommen
Richtig wäre m = - 0,5
m = ( y2 - y1 ) / ( x2 - x1 ) = ( - 1 - 4 ) / ( 6 - ( - 4 ) ) = - 5 / 10 = - 0,5
und danach habe ich das in y = mx+n eingesetzt, also die -4 für y dann für das m die 0,5 * 4
Warum setzt du die x-Koordinate -4 des Punktes A für y ein? Richtig wäre, die y-Koordinate von A , also 4 , für y einzusetzen und die x-Koordiante von A, also - 4 , für x sowie - 0,5 für m. Du erhältst dann:
4 = ( - 0,5 ) * ( - 4 ) + n
<=> 4 = 2 + n
<=> n = 4 - 2
<=> n = 2
Und nun setzt du m = - 0,5 und n = 2 in die allgemeine Geradengleichung y = m x + n ein und erhältst:
y = - 0,5 * x + 2
Und das ist die Gleichung der Geraden, die durch die Punkte A und B verläuft. Probe durch Einsetzen der Koordinaten, z.B. Punkt B ( 6 | - 1 ) :
- 1 = - 0,5 * 6 + 2
<=> - 1 = -1
Das ist eine immer wahre Aussage, also liegt der Punkt B auf der Geraden.
Kann ich das da direkt in y = mx + n einsetzen? also 9 für y und Anstieg 1 ist ja sozusagen m stimmts? und x ist eben 4
Richtig! Du erhältst:
9 = 1 * 4 + n
Auflösen nach n:
n = 9 - 4 = 5
also Geradengleichung:
y = 1 x + 5
Probe:
9 = 1 *4 + 5
<=> 9 = 9
Immer wahre Aussage, also liegt C auf der Geraden.
Den Schnittpunkt musste ich auch berechnen, ... war das jetzt der Punkt wo die Gerade durch die x-Achse geht oder wo sich 2 Geraden schneiden?
Nun, ein Schnittpunkt ist ein Punkt, in dem sich zwei oder mehr Graphen schneiden. Das können zwei Geraden sein, oder eine Gerade und eine Koordinatenachse oder irgendwelche anderen Kurven.
Den Schnittpunkt einer Geraden mit der x-Achse nennt man auch x-Achsenabschnitt.
Wenn verlangt wird, einen Schnittpunkt zu berechnen, dann muss auch dazugesagt werden, von welchen Graphen, sofern sich das nicht aus dem Zusammenhang ergibt.
Ich nehme an, dass vorliegend der Schnittpunkt der beiden Geraden berechnet werden soll, deren Gleichungen oben bestimmt wurden.
Wie rechne ich nun y aus?
Indem du den berechneten x-Wert in eine der beiden Geradengleichungen einsetzt (welche du nimmst, ist gleichgültig, da der Schnittpunkt ja zu beiden Geraden gehört und sich daher bei beiden Geradengleichungen derselbe y-Wert ergeben muss)
keine ahnung woher die -26,57° aufeinmal kommen
Betrachte dazu folgende Skizze:
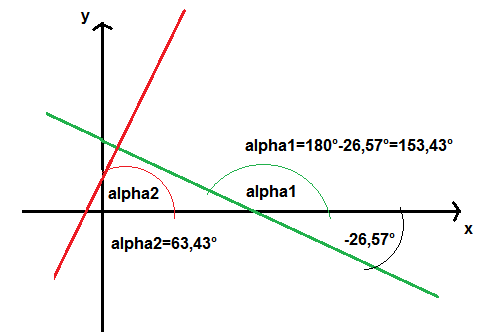
Die - 26,57° ergeben sich, indem man auf beide Seiten der Gleichung
m = tan (alpha1)
die Umkehrfunktion des Tangens, also die Funktion arctan ( x ) anwendet ("Arkustangens").
Dadurch ergibt sich:
arctan ( m ) = arctan ( tan ( alpha1) )
<=> arctan ( m ) = alpha1
Mit m = - 0,5 ergibt sich:
alpha1 = arctan ( - 0,5 ) = - 26,57°
Nun liefert die Funktion arctan ( x ) immer die Größe des kleineren Winkels zwischen Gerade und x-Achse, also vorliegend die Größe des Winkels, in den ich die - 26,57° geschrieben habe. Will man stattdessen die Größe des anderen Winkels, den ich in der Skizze mit alpha1 bezeichnet habe, wissen, so muss man zu dem Wert, den die arctan-Funktion liefert noch 180° addieren und kommt so auf
alpha1 = - 26,57° + 180° = 153, 43°
Der andere Winkel alpha2 ist der Winkel zwischen der zweiten Geraden
e : y = 2 x + 1
und der x-Achse. Hier ist der Winkel alpha2 kleiner als sein Nebenwinkel, also liefert die Funktion arctan ( m ) für m = 2 direkt den gesuchten Winkel alpha2. Es ergibt sich:
alpha2 = arctan ( 2 ) = 63.,43°
Merke: Ist die Steigung m negativ (wie bei der Geraden g), dann muss man zu dem Wert, den die arctan-Funktion liefert, 180 ° addieren, um die Größe des in mathematisch positiver Richtung (entgegen dem Urzeigersinn) gesehenen Winkels zwischen x-Achse und Gerade zu erhalten. Ist m hingegen positiv, dann liefert arctan ( m ) direkt die Größe des in mathematisch positiver Richtung gesehenen Winkels zwischen der x-Achse und der Geraden.