Wie finde ich geeignete Beispiele in Teilaufgabe 2 und 3 wo die Ungleichung strikt ist(Beweise hab ich schon)?

Question

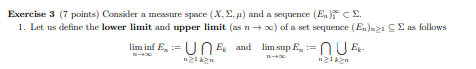
Text erkannt:

Exercise 3 ( 7 points) Consider a measure space \( (X, \Sigma, \mu) \) and a sequence \( \left(E_{n}\right)_{1}^{\infty} \subset \Sigma \).
1. Let us define the lower limit and upper limit (as \( n \rightarrow \infty) \) of a set sequence \( \left(E_{n}\right)_{n \geq 1} \subseteq \Sigma \) as follows
\( \underset{n \rightarrow \infty}{\liminf } E_{n}:=\bigcup_{n \geq 1} \bigcap_{k \geq n} E_{k} \text { and } \limsup _{n \rightarrow \infty} E_{n}:=\bigcap_{n \geq 1} \bigcup_{k \geq n} E_{k} \)

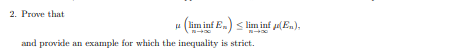
Text erkannt:

2. Prove that
\( \mu\left(\liminf _{n \rightarrow \infty} E_{n}\right) \leq \liminf _{n \rightarrow \infty} \mu\left(E_{n}\right), \)
and provide an example for which the inequality is strict.

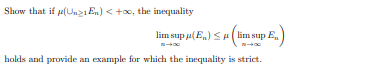
Text erkannt:

Show that if \( \mu\left(\cup_{n \geq 1} E_{n}\right)<+\infty \), the inequality
\( \limsup _{n \rightarrow \infty} \mu\left(E_{n}\right) \leq \mu\left(\limsup _{n \rightarrow \infty} E_{n}\right) \)
holds and provide an example for which the inequality is strict.

Answer 1

Um solch ein Beispiel zu finden, ist es wohl am einfachsten zu überprüfen, in welchem Schritt des Beweises eigentlich diese Ungleichung zustande kommt. Für 2) ist das
der Schritt
\(\begin{aligned} \lim_{n \to \infty } \mu\biggl( \bigcap_{ k\geqslant n}^{ } E_{ k} \biggr) \leqslant \lim_{ n \to\infty} \inf_{ k\geqslant n} \mu( E_{ k} ) .\end{aligned}\)
Also müssen wir \( ( E_{ k} ) _{ k\geqslant 1} \) finden, sodass
\(\begin{aligned} \mu\biggl( \bigcap_{ k\geqslant n}^{ } E_{ k} \biggr)< \inf_{ k\geqslant n} \mu( E_{ k} ) \end{aligned}\)
gilt (und sogar im Limes für \( n \to \infty \)). Wenn z.B. die \( E_{ k} \) disjunkt sind, so ist die linke Seite immer Null, ein Beispiel wäre also
der Massraum \( ( \mathbf{R}, \mathcal{B}( \mathbf{R}) ) \) und \( E_{ k}  = [ k, k + 1] \).