Tangentengleichung im Punkt P finden

Question

Aufgabe:

Geben Sie die Gleichung der Tangente an den Graphen f im Punkt P(1|f(1)) an

a) x^4

b) 1/x

c) √x

Problem/Ansatz:

Wie soll man das berechnen?

Answer 1

f ( x ) = x^4
f ( 1 ) = 1
P ( 1 | 1)

f ´ ( x ) = 4 * x^3
f ´ ( 1 ) = 4 = m ( Tangente )

Tangente
y = m * x + b
( 1 | 1 )
1 = 4 * 1 + b
b = 1 - 4 = -3

y ( x ) = 4 * x - 3

Answer 2

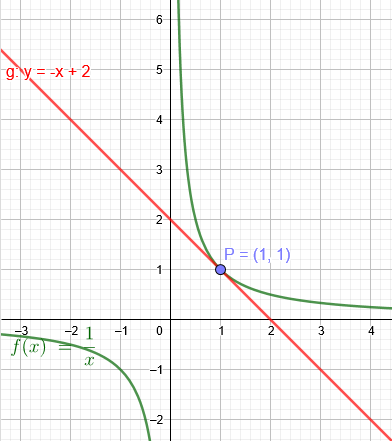
Geben Sie die Gleichung der Tangente an den Graphen f im Punkt P(1|f(1)) an:
b) f(x)=\( \frac{1}{x} \)

f(1)=\( \frac{1}{1} \)=1     →   P(1|1)

f´(x)=-\( \frac{1}{x^2} \)

f´(1)=-\( \frac{1}{1} \)=-1

\( \frac{y-y_1}{x-x_1} \)=m

\( \frac{y-1}{x-1} \)=-1

y-1=-x+1

y=-x+2