Aufgabe:
Text erkannt:
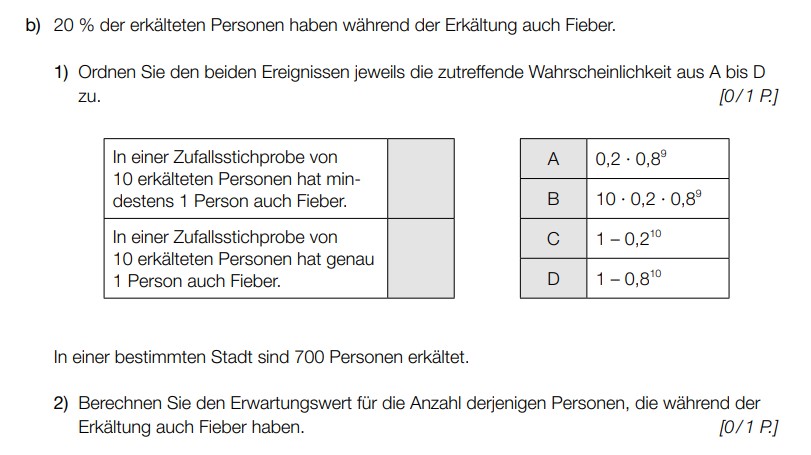
b) 20 \% der erkälteten Personen haben während der Erkältung auch Fieber.
1) Ordnen Sie den beiden Ereignissen jeweils die zutreffende Wahrscheinlichkeit aus A bis \( D \) zu.
[0/1 P.]
\begin{tabular}{|l|l|}
\hline \( \begin{array}{l}\text { In einer Zufallsstichprobe von } \\ 10 \text { erkälteten Personen hat min- } \\ \text { destens } 1 \text { Person auch Fieber. }\end{array} \) & \\
\hline In einer Zufallsstichprobe von & \\
10 erkälteten Personen hat genau & \\
1 Person auch Fieber. & \\
\hline
\end{tabular}
\begin{tabular}{|l|l|}
\hline\( A \) & \( 0,2 \cdot 0,8^{9} \) \\
\hline\( B \) & \( 10 \cdot 0,2 \cdot 0,8^{9} \) \\
\hline\( C \) & \( 1-0,2^{10} \) \\
\hline\( D \) & \( 1-0,8^{10} \) \\
\hline
\end{tabular}
In einer bestimmten Stadt sind 700 Personen erkältet.
2) Berechnen Sie den Erwartungswert für die Anzahl derjenigen Personen, die während der Erkältung auch Fieber haben.
[0/1 P.]
Problem/Ansatz:
Kann mir jemand erklären was da stimmt ich bräuchte auch eine Erklärung danke