Wie hoch ist das Kreuz auf einem 61 m hohen Kirchturm, wenn es mit einem Theodoliten, der 100 m vom Fuß des Turmes …

Question

Aufgabe:

3. Wie hoch ist das Kreuz auf einem 61 m hohen Kirchturm, wenn es mit einem Theodoliten, der 100 m vom Fuß des Turmes und 1 m über dem Niveau des Turmfußes steht, unter einem Sehwinkel von 1.5 gesehen wird?

Answer 1

Hast du dir bereits eine Skizze gemacht?

TAN(α°) = 60/100 --> α = 30.96375653°

TAN((30.96375653 + 1.5)°) = (60 + h)/100 --> h = 3.618131797 m

Skizze

Answer 2

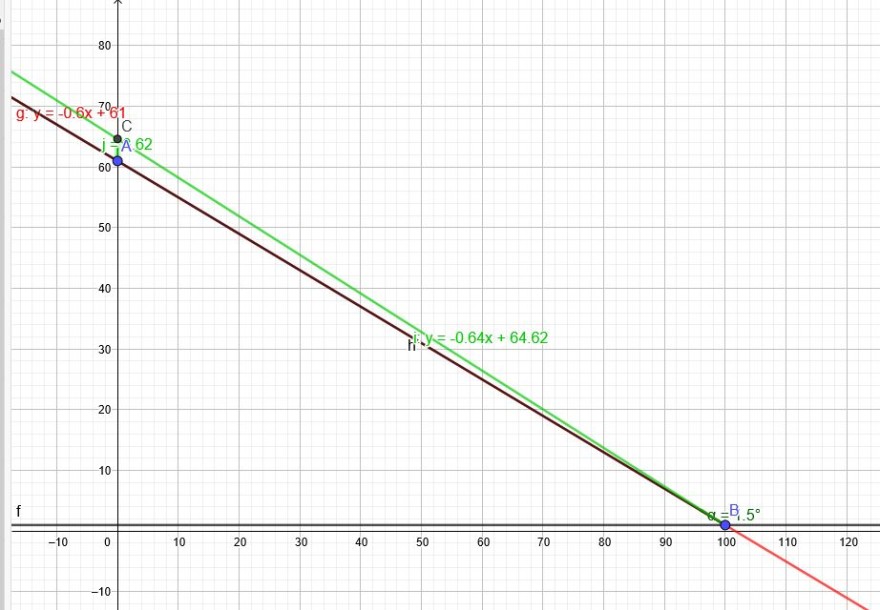
3. Wie hoch ist das Kreuz auf einem 61 m hohen Kirchturm, wenn es mit einem Theodoliten, der 100 m vom Fuß des Turmes und 1 m über dem Niveau des Turmfußes steht, unter einem Sehwinkel von 1.5 gesehen wird?

\(B(100|1)\)   \(A(0|61)\) Gerade durch B und A:

\( \frac{61-1}{0-100}=\frac{y-1}{x-100} \)

\( \frac{y-1}{x-100}=-\frac{3}{5} \)

\(y=-\frac{3}{5}x+61\)  →   \( m_1=-\frac{3}{5} \)   →\( tan^{-1}(-\frac{3}{5})=-30,96° \)

neuer Winkel: \(=-30,96°-1,5°=-32,46° \)

\(tan (-32,46°)=-0,636\)

Gerade durch  \(B(100|1)\):

\( \frac{y-1}{x-100}=-0,636 \)  Nun an der Stelle\(x=0\)

\( \frac{y-1}{-100}=-0,636 \)

\( y=64,6 \)

Kreuzhöhe:

\( 64,6-61=3,6m \)