Ermitteln Sie, wie hoch das Kreuz auf der Spitze eines Turmes ist. Wie viel Meter ist der Ballon gestiegen?

Question

1. Ermitteln Sie, wie hoch das Kreuz auf der Spitze eines \( 53 \mathrm{~m} \) hohen Turmes ist, wenn es in einer waagrechten Entfernung von \( 100 \mathrm{~m} \) vom Fußpunkt des Turmes unter dem Sehwinkel von \( 0,54^{\circ} \) erscheint.

2. Von einem Beobachtungsort, der vom Aufstiegsplatz eines Ballons \( 265 \mathrm{~m} \) (530 m) entfernt ist, wird der genau senkrecht aufsteigende Ballon unter dem Höhenwinkel von \( \alpha=37,2^{\circ}\left(45,2^{\circ}\right) \) und einige Zeit später unter dem Höhenwinkel \( \beta=72,3^{\circ}\left(71,3^{\circ}\right) \) gesehen. Bestimmen Sie, um wie viel Meter der Ballon inzwischen gestiegen ist.

Answer 1

Zur Aufgabe 1:

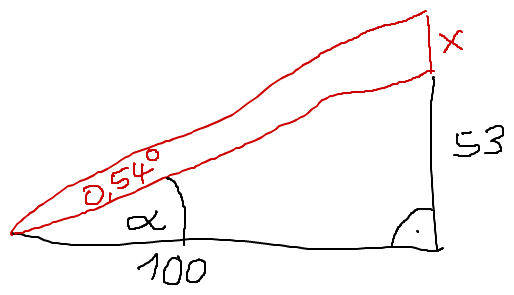
tan(alpha) = 53/100  also alpha = 27,92°

tan(27,92° +0,54° ) = (x+53) / 100

0,5421= (x+53) / 100

54,21=x+53

x=1,21

Zur Aufgabe 2:

1. Höhe= h

dann ist tan(37,2°) = h/265  also h=194,3

jetzt kommt die 2. Messung: gesamthöhe=h1

tan(72,3°)=h1 / 265   also h1=830,4

also zwischendurch 830,4 - 194,3 aufgestiegen