Bestimmen Sie, um wie viele Meter der Ballon inzwischen gestiegen ist.

Question

Von einem Beobachtungsort, der vom Austiegsplatz eines Ballons 265 m (530 m) entfernt ist, wird der genau senkrecht aufsteigende Ballon unter dem Höhenwinkel von Alpha= 37,2° (45,2°) und einige Zeit später unter dem Höhenwinkel Beta= 72,3° (71,3°) gesehen.

Bestimmen Sie, um wie viele Meter der Ballon inzwischen gestiegen ist.

(Angaben für b) jeweils in Klammern.

Ansatz/Problem:

Ich wäre sehr dankbar für eine passende Skizze und den Rechenweg.

Answer 1

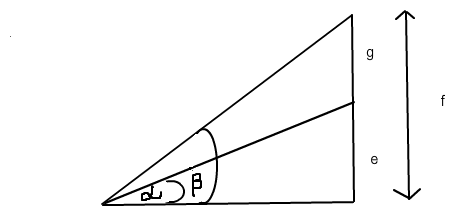
1. Höhe des Ballons:  tan (α) = e / 265,  e = 265 * tan (α)

2. Höhe des Ballons:  tan (β) = f / 265,   f = 265 * tan (β)

Steighöhe g  =  f - e

= 265 * tan (β) - 265 * tan (α)

= 265 * (tan (72,3°) - tan (37,2°))

≈ 629,2m

Der Ballon ist also um etwa 629,2m gestiegen.

Aufgabe b geht natürlich analog.

Das Ergebnis zur Kontrolle:  ≈ 1032,1m

:)

Answer 2

Wie kommts du auf den Winkel gamma = 35.1 °

Der Winkel gamma müßte 90 - 37.2 ° betragen .

Ansonnsten kann auch gerechnet werden
( im rechtwinkligen Dreieck )

tan 37.2 = H / 265

Answer 3

H = sin(37,2°) * 265 / sin(35,1° )
gibt ungefähr 278,6