Aufgabe:
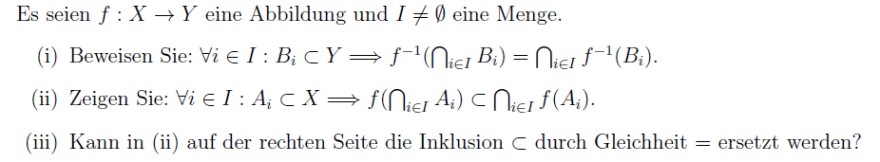
Text erkannt:
Es seien \( f: X \rightarrow Y \) eine Abbildung und \( I \neq \emptyset \) eine Menge.
(i) Beweisen Sie: \( \forall i \in I: B_{i} \subset Y \Longrightarrow f^{-1}\left(\bigcap_{i \in I} B_{i}\right)=\bigcap_{i \in I} f^{-1}\left(B_{i}\right) \).
(ii) Zeigen Sie: \( \forall i \in I: A_{i} \subset X \Longrightarrow f\left(\bigcap_{i \in I} A_{i}\right) \subset \bigcap_{i \in I} f\left(A_{i}\right) \).
(iii) Kann in (ii) auf der rechten Seite die Inklusion \( \subset \) durch Gleichheit \( = \) ersetzt werden?
Problem/Ansatz:
Hey Leute, für die Aufgabe i hatte ich mir gedacht ich beweise die Aussage von links nach rechts und rechts nach links indem ich annehme, das eine x Teil des Urbilds ist. Kann mir da einer helfen ?
Für 2 und 3 habe ich keine Ahnung wie ich das machen soll. Liebe Grüße :)