Extremalproblem Anschlusspunkt Mathe

Question

Aufgabe:

Zwischen Flugplatz, Wald und nördlichem Flussrand, der für 0≤x≤ 12 durch die
Funktion f(x) = 12x-x + 5 beschrieben
wird, soll ein achsenparalleles, dreieckiges Gelände A für die Flughafenfeuerwehr angelegt werden.
Wie muß der Anschlusspunkt P(x|f(x)) am Fluss gewählt werden, damit der Platz A möglichst groß wird?

Problem/Ansatz:

Ich habe bei vielen gesehen, dass sie immer für a zum Beispiel 5 - f(x) angegeben haben und für b (12-x). Mein Problem ist es, warum mein minus rechnet also 5 - f(x) .. ich verstehe es nicht.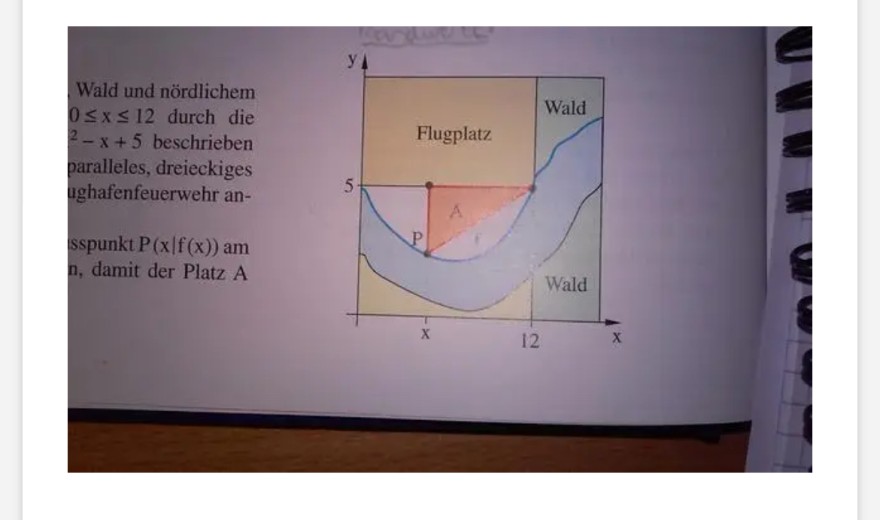

Text erkannt:

Wald und nördlichem $0 \leq x \leq 12$ durch die $2-x+5$ beschrieben paralleles, dreieckiges ughafenfeuerwehr ansspunkt $P(x \mid f(x))$ am n, damit der Platz A

Comments

Wie genau lautet die Funktion f(x)?

---

Lautet die Funktion nicht $f(x)=\frac{1}{12}x^2-x+5$  ? Das passt besser zum Bild.

Answer 1

Zwischen Flugplatz, Wald und nördlichem Flussrand, der für $0≤x≤ 12$ durch die Funktion             $f(x)=\frac{1}{12}x^2-x+5$ beschrieben wird, soll ein achsenparalleles, dreieckiges Gelände A für die Flughafenfeuerwehr angelegt werden.
Wie muss der Anschlusspunkt $P(x|f(x))$ am Fluss gewählt werden, damit der Platz A möglichst groß wird?

$A= \frac{1}{2}\cdot (12-x)\cdot (5-f(x))$ soll maximal werden.

Die Zeichnung zeigt dir noch den Sachverhalt:

Answer 2

Hallo,

gesucht ist der größte Flächeninhalt des Dreiecks APC. Die Formel lautet $A_{Dreieck}=\frac{g\cdot h}{2}$.

g = Strecke AC = 12 - x

h = Strecke AP = 5 - f(x)

Ist x beispielsweise 3, dann ist g = 12 - 3 = 9 und h ist 5 - f(3) (= 2,75) = 2,25

Bilde also die 1. Ableitung A' von der Formel für den Flächeninhalt, setze sie = 0 und löse nach x auf.

$A_{Dreieck}=\frac{(12-x)\cdot (5-(\frac{1}{12}x^2-x+5)}{2}$

Gruß, Silvia