Aufgabe: Hallo. Hat jemand die Lösungen zu diesen Abituraufgaben? Ich bin ser verzweifelt und bräuchte die Lösungen dazu. Herzlichen Dank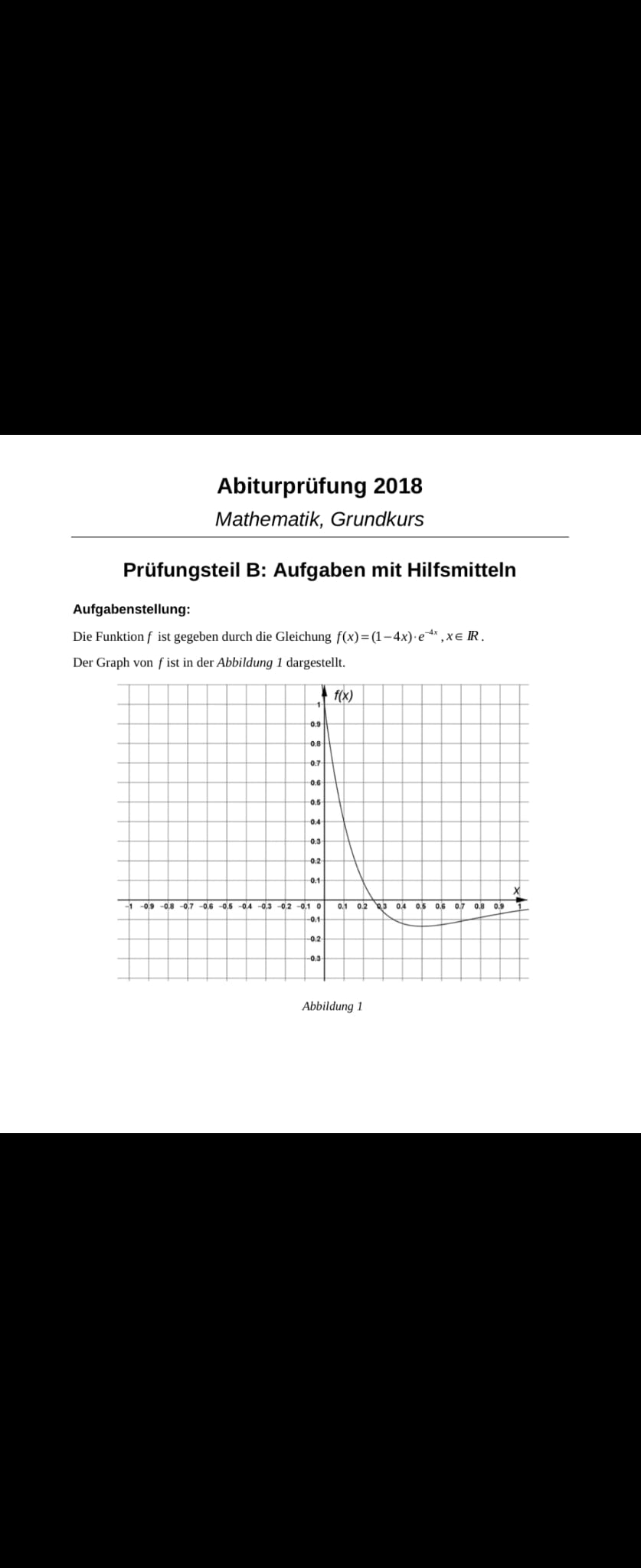
Text erkannt:
Abiturprüfung 2018
Mathematik, Grundkurs
Prüfungsteil B: Aufgaben mit Hilfsmitteln
Aufgabenstellung:
Die Funktion \( f \) ist gegeben durch die Gleichung \( f(x)=(1-4 x) \cdot e^{-4 x}, x \in \mathbb{R} \).
Der Graph von \( f \) ist in der Abbildung 1 dargestellt.
Abbildung 1

Text erkannt:
Ministerium für
Schule und Bildung
des Landes Nordrhein-Westfalen
M GK NT B1 GTR (GG)
Seite 2 von 3
Name:
a) (1) Zeigen Sie, dass \( x=0,25 \) die einzige Nullstelle der Funktion \( f \) ist, und begründen Sie, dass \( f(x)<0 \) für \( x>0,25 \).
(2) Bestimmen Sie rechnerisch die Koordinaten des globalen Extrempunktes E des Graphen vonf.
[Zur Kontrolle: \( f^{\prime}(x)=-4(2-4 x) \cdot e^{-4 x} \).]
(3) Zeigen Sie, dass \( F \) mit \( F(x)=x \cdot e^{-4 x}, x \in \mathbb{R} \), eine Stammfunktion von \( f \) ist.
(4) Durch Spiegelung des Graphen der Funktion \( f \) an der \( y \)-Achse entsteht der Graph der Funktion \( f^{*} \).
Skizzieren Sie den Graphen der Funktion \( f^{*} \) in der Abbildung 1 und geben Sie eine Funktionsgleichung der Funktion \( f^{*} \) an.
\( (4+9+2+4 \text { Punkte) } \)
b) (1) Die Funktion \( f \) schließt im ersten Quadranten mit der \( x \) - und der \( y \)-Achse die Fläche \( A_{f} \) ein.
Bestimmen Sie die Größe der Fläche A, auf drei Nachkommastellen gerundet.
[Kontrolllösung mit zwei Nachkommastellen: \( A_{f} \approx 0,09 \) [FE].]
(2) Erläutern Sie, dass für alle \( u>0,25 \) gilt: \( \int \limits_{0}^{u} f(x) \mathrm{d} x<A_{f} \), und bestimmen Sie eine obere Integrationsgrenze \( u>0,25 \) so, dass gilt: \( \int \limits_{0}^{u} f(x) \mathrm{d} x=\frac{1}{2} A_{t} \).
(3) Der Punkt \( P(r \mid f(r)) \) mit \( 0 \leq r \leq 0,25 \) ist ein Punkt des Graphen von \( f \). Gemeinsam mit den Punkten \( A(r \mid 0), B(0 \mid f(r)) \) und dem Koordinatenursprung bildet
Text erkannt:
Ministerium für
Schule und Bildung
des Landes Nordrhein-Westfalen
M GK NT B1 GTR (GG)
Seite 3 von 3
Name:
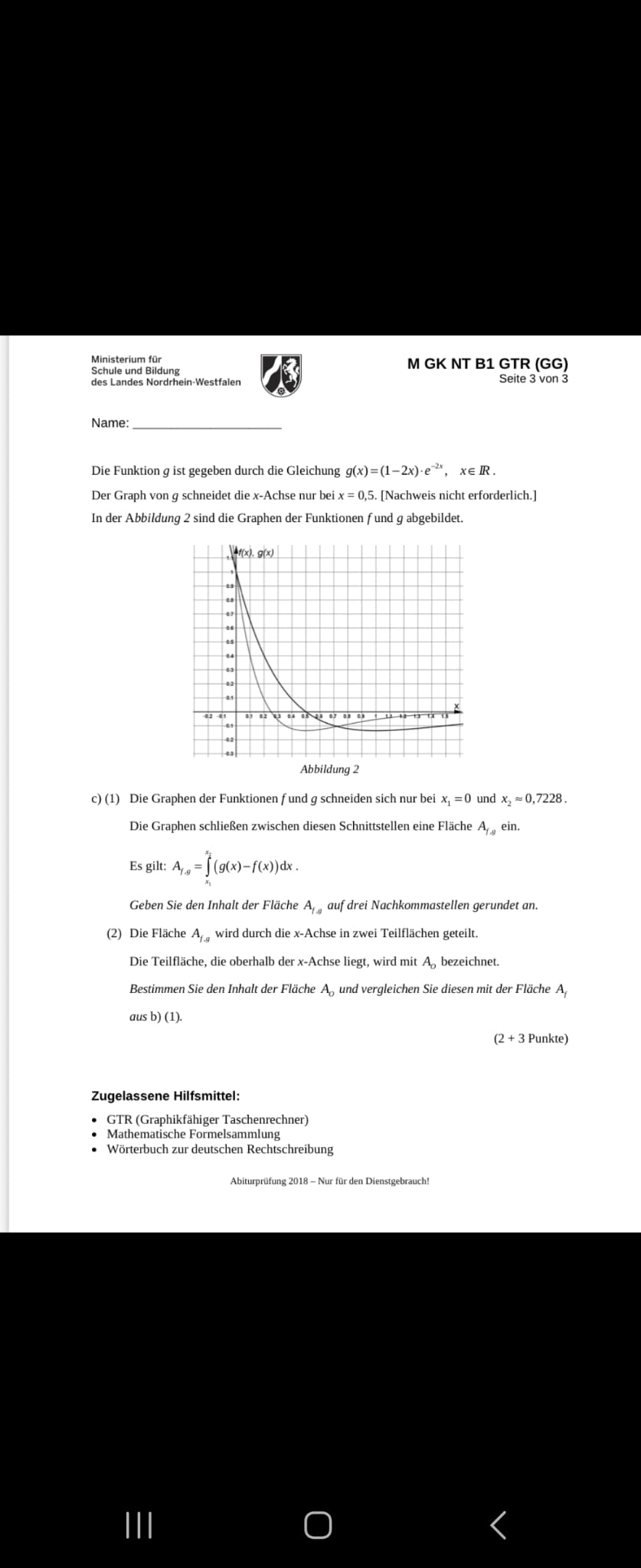
Die Funktion \( g \) ist gegeben durch die Gleichung \( g(x)=(1-2 x) \cdot e^{-2 x}, \quad x \in \mathbb{R} \).
Der Graph von \( g \) schneidet die \( x \)-Achse nur bei \( x=0,5 \). [Nachweis nicht erforderlich.] In der Abbildung 2 sind die Graphen der Funktionen \( f \) und \( g \) abgebildet.
Abbildung 2
c) (1) Die Graphen der Funktionen \( f \) und \( g \) schneiden sich nur bei \( x_{1}=0 \) und \( x_{2} \approx 0,7228 \). Die Graphen schließen zwischen diesen Schnittstellen eine Fläche \( A_{f_{g}} \) ein.
Es gilt: \( A_{f, g}=\int \limits_{x_{1}}^{x_{2}}(g(x)-f(x)) \mathrm{d} x \).
Geben Sie den Inhalt der Fläche \( A_{f, g} \) auf drei Nachkommastellen gerundet an.
(2) Die Fläche \( A_{f g} \) wird durch die \( x \)-Achse in zwei Teilflächen geteilt.
Die Teilfläche, die oberhalb der \( x \)-Achse liegt, wird mit \( A_{0} \) bezeichnet.
Bestimmen Sie den Inhalt der Fläche \( A_{o} \) und vergleichen Sie diesen mit der Fläche \( A_{f} \) aus b) (1).
\( (2+3 \) Punkte)
Zugelassene Hilfsmittel:
- GTR (Graphikfähiger Taschenrechner)
- Mathematische Formelsammlung
- Wörterbuch zur deutschen Rechtschreibung
Abiturprüfung 2018 - Nur für den Dienstgebrauch!
Hallo