Eine zur y-Achse symmetrische Parabel hat den Scheitelpunkt \(S(0|9)\) und geht durch den Punkt \(A (6|0)\). Dem Parabelsegment, das durch die x-Achse begrenzt wird, ist ein Trapez mit maximaler Fläche einzuschreiben.
Berechne den Flächeninhalt des Trapezes. (Angaben in cm).
\(f(x)=a*x^2+9\)
\(A (6|0)\):
\(f(6)=a*36+9=0\) → \(a=-\frac{1}{4}\)
\(f(x)=-\frac{1}{4}*x^2+9\)
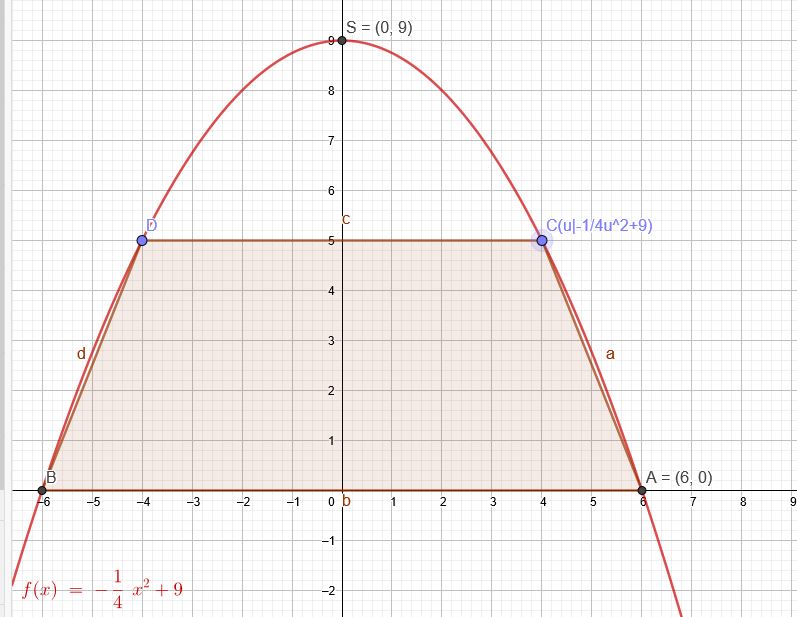
\(A(u)=\frac{1}{2}\cdot(12+2u) \cdot (-\frac{1}{4}*u^2+9) \)soll maximal werden.
Ausmultiplizieren
\(A´(u)=0 \)
\(u=...\)
Flächeninhalt berechnen