Folge Divergent oder Konvergent

Question

Aufgabe:

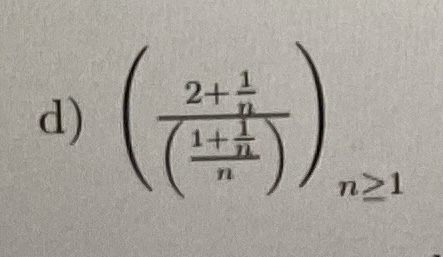
Text erkannt:

d) $\left(\frac{2+\frac{1}{n}}{\left(\frac{1+\frac{1}{n}}{n}\right)}\right)_{n \geq 1}$

Hi noch einmal.

Diese Folge soll anhand der Grenzwertsätze untersucht werden ob sie konvergent ist, gegebenenfalls soll der Grenzwert berechnet werden. Problem ist, dass ich zwar den Term zu (2n+1)/(1+1/n) ungeformt habe, der Grenzwert für n gegen unendlich am Ende der Rechnung jedoch 2n beträgt. Bedeutet dies, dass die Folge divergent ist ? Wie könnte ich das den beweisen ?

Ich hoffe sehr die Frage klingt nicht allzu dumm, aber ich finde echt den Zusammenhang nicht.

Answer 1

"der Grenzwert für n gegen unendlich am Ende der Rechnung jedoch 2n beträgt"

Besser so formuliert:

Die Folge verhält sich für große Werte von n wie der Term 2n+1,

also nach oben unbeschränkt ==>   divergent.

Manche Leute sagen auch:

bestimmt divergent gegen +∞.

Answer 2

Post zurückgenommen. Hast Recht mit der Divergenz.

Comments

Das ist falsch. Der Zähler geht bei Dir gegen 2, der Nenner gegen 0. Das ist Divergenz.

---

Vielen Dank für die Anmerkung, habe Post zurückgenommen.